Загадка про заключенных в шляпах: 4 человека в шляпах | Математические задачи
Интересные задачи на логику
Эти задачи можно решить с ходу, жуя бутерброд в обеденный перерыв. А можно сломать весь мозг, но так и не сообразить, где тут правда и в чем подвох. Ответы внизу страницы.
1. Загадка о заключенных
4 заключенных приговорены к казни.
На них надели две белые шляпы и две черные шляпы. Мужчины не знают, какого цвета шляпы они носят. Четверых заключенных выстроили друг за другом (см. рисунок) таким образом, что:
Заключенный № 1 может видеть заключенных № 2 и № 3.
Заключенный № 2 может видеть заключенного № 3.
Заключенный № 3 не видит никого.
Заключенный № 4 не видит никого.
Судья любому заключенному, назвавшему цвет своей шляпы, пообещал свободу.
Вопрос: Кто назвал цвет своей шляпы первым?
2. Трудности на дороге
Один человек, меняя колесо у своей машины, уронил все 4 гайки крепления в решетку канализационного стока. Достать их оттуда невозможно. Водитель уже решил, что застрял на дороге надолго, но тут проходящий мимо ребенок посоветовал, как закрепить колесо. Водитель последовал совету и спокойно доехал до ближайшей шиномонтажки.
Водитель последовал совету и спокойно доехал до ближайшей шиномонтажки.
Вопрос: Что посоветовал ребенок?
3. Явка провалена
Человеку нужно было проникнуть в секретный клуб, не вызвав подозрений. Он заметил, что все приходящие сначала отвечали на вопросы охранника и лишь затем входили. Первому пришедшему был задан вопрос: «22?» Он ответил: «11!» — и прошел. Второму: «28?» Ответ был: «14». И тоже оказался верным. Человек решил, что все просто, и смело подошел к охраннику. «42?» — спросил охранник. «21!» — уверенно ответил человек и сразу же был изгнан.
Вопрос: Почему?
4. Подарок Бабы-яги
Лето уже закончилось, когда Иван-царевич, направлявшийся в тридевятое царство за невестой, попросил ночлега в избушке на курьих ножках. Баба-яга ласково встретила гостя, напоила, накормила, спать уложила. На следующее утро она проводила Ивана-царевича с таким напутствием: «Встретится тебе по дороге река, моста через нее нет — придется тебе плыть. Возьми этот волшебный кафтан. Наденешь его — и бросайся смело в реку, кафтан не даст утонуть». Сто дней и ночей шел Иван-царевич и добрался наконец до реки. Но, чтобы преодолеть ее, кафтан ему не понадобился.
Возьми этот волшебный кафтан. Наденешь его — и бросайся смело в реку, кафтан не даст утонуть». Сто дней и ночей шел Иван-царевич и добрался наконец до реки. Но, чтобы преодолеть ее, кафтан ему не понадобился.
Вопрос: Почему?
5. Клетки с кроликами
Во дворе стояли в ряд 3 большие клетки, окрашенные в разные цвета: красный, желтый и зеленый. В клетках жили кролики, причем в зеленой их было вдвое больше, чем в желтой. Однажды из левой клетки взяли 5 кроликов для живого уголка, а половину оставшихся перевели в красную клетку.
Вопрос: Какого цвета была левая клетка?
6. Кто виноват?
Поздно вечером в одном из переулков неизвестная машина сбила человека и скрылась. Постовой милиционер обратил внимание, что автомобиль двигался с большой скоростью. 6 человек, оказавшихся неподалеку, сообщили противоречивые сведения: «Машина синего цвета, за рулем был мужчина».«Машина шла на большой скорости и с погашенными фарами». «Машина была с номерным знаком и шла не очень быстро». «Машина „Москвич“ шла с погашенным светом». «Машина без номерного знака, за рулем была женщина».«Машина „Победа“, серого цвета».
«Машина была с номерным знаком и шла не очень быстро». «Машина „Москвич“ шла с погашенным светом». «Машина без номерного знака, за рулем была женщина».«Машина „Победа“, серого цвета».
Когда задержали автомобиль, выяснилось, что лишь один свидетель сообщил верные сведения. Остальные пятеро — по одному правильному и одному неправильному факту.
Назовите марку, цвет и скорость автомобиля. Имела ли машина номерной знак, шла ли она со светом и кто ее вел: мужчина или женщина?
7. Бонус
Так что же делают одновременно все люди на Земле?
Ответы:
- 4-й и 3-й заключенные молчат, потому что вообще ничего не видят. 1-й заключенный молчит, потому что видит перед собой шляпы разного цвета: у 2-го и 3-го. Соответственно у него либо белая, либо черная шляпа. 2-й заключенный, понимая, что 1-й молчит, делает вывод о том, что у него шляпа не такого цвета, как у 3-го, а именно белого цвета. Вывод: Первым назвал цвет своей шляпы заключенный № 2.

- Отвернуть по 1 гайке от оставшихся 3 колес и закрепить ими 4-е.
- На первый взгляд кажется, что пароль — это результат деления названного числа на 2. На самом деле это количество букв в предложенных числах. Верный ответ не 21, а 8.
- Иван-царевич был у Бабы-яги в сентябре. Отсчитываем 100 дней и узнаем, что зима уже в разгаре. Река скована льдом, и ее можно спокойно перейти и без кафтана.
- Клетка была желтая. Задача подсказывает, что в зеленой клетке кроликов было вдвое больше — следовательно, их там четное количество. После того как из левой клетки забрали пятерых, в ней осталось тоже четное количество (так как легко разделилось пополам). Значит, до взятия количество кроликов было нечетным. Таким образом, левая клетка — не зеленая. Но и не красная, что видно из условия задачи.
- Это была «Победа», синего цвета, с номерным знаком. Шла на большой скорости и с погашенными фарами. За рулем была женщина. Ориентируемся на показания постового — высокая скорость автомобиля.
 Зная, что свидетельство о низкой скорости заведомо неверное, определяем оставшиеся варианты.
Зная, что свидетельство о низкой скорости заведомо неверное, определяем оставшиеся варианты. - Становятся старше.
По материалам Smekalka
Поделитесь с друзьями!
4 заключенных приговоренных к казни в шляпах. Интересные задачи на логику. Загадка о заключенных
Ребята, мы вкладываем душу в сайт. Cпасибо за то,
что открываете эту
красоту. Спасибо за вдохновение и мурашки.
Присоединяйтесь к нам в Facebook
и ВКонтакте
Эти задачи можно решить с ходу, жуя бутерброд в обеденный перерыв. А можно сломать весь мозг, но так и не сообразить, где тут правда и в чем подвох.
Предлагаем вам вместе с сайт
размять извилины и пощелкать логические задачи, словно орешки.
1. Загадка о заключенных
4 заключенных приговорены к казни.
На них надели две белые шляпы и две черные шляпы. Мужчины не знают, какого цвета шляпы они носят. Четверых заключенных выстроили друг за другом (см. рисунок) таким образом, что:
Заключенный № 1 может видеть заключенных № 2 и № 3.
Заключенный № 2 может видеть заключенного № 3.
Заключенный № 3 не видит никого.
Заключенный № 4 не видит никого.
Судья любому заключенному, назвавшему цвет своей шляпы, пообещал свободу.
Вопрос:
Кто назвал цвет своей шляпы первым?
4-й и 3-й заключенные молчат, потому что вообще ничего не видят.
1-й заключенный молчит, потому что видит перед собой шляпы разного цвета: у 2-го и 3-го. Соответственно у него либо белая, либо черная шляпа.
2-й заключенный, понимая, что 1-й молчит, делает вывод о том, что у него шляпа не такого цвета, как у 3-го, а именно белого цвета.
Вывод:
Первым назвал цвет своей шляпы заключенный № 2.
2. Трудности на дороге
Один человек, меняя колесо у своей машины, уронил все 4 гайки крепления в решетку канализационного стока. Достать их оттуда невозможно. Водитель уже решил, что застрял на дороге надолго, но тут проходящий мимо ребенок посоветовал, как закрепить колесо. Водитель последовал совету и спокойно доехал до ближайшей шиномонтажки.
Вопрос:
Что посоветовал ребенок?
3. Явка провалена
Человеку нужно было проникнуть в секретный клуб, не вызвав подозрений. Он заметил, что все приходящие сначала отвечали на вопросы охранника и лишь затем входили. Первому пришедшему был задан вопрос: «22?» Он ответил: «11!» — и прошел. Второму: «28?» Ответ был: «14». И тоже оказался верным. Человек решил, что все просто, и смело подошел к охраннику. «42?» — спросил охранник. «21!» — уверенно ответил человек и сразу же был изгнан.
Вопрос:
Почему?
4. Подарок Бабы-яги
Лето уже закончилось, когда Иван-царевич, направлявшийся в тридевятое царство за невестой, попросил ночлега в избушке на курьих ножках. Баба-яга ласково встретила гостя, напоила, накормила, спать уложила. На следующее утро она проводила Ивана-царевича с таким напутствием: «Встретится тебе по дороге река, моста через нее нет — придется тебе плыть. Возьми этот волшебный кафтан. Наденешь его — и бросайся смело в реку, кафтан не даст утонуть». Сто дней и ночей шел Иван-царевич и добрался наконец до реки. Но, чтобы преодолеть ее, кафтан ему не понадобился.
Сто дней и ночей шел Иван-царевич и добрался наконец до реки. Но, чтобы преодолеть ее, кафтан ему не понадобился.
Вопрос:
Почему?
5. Клетки с кроликами
Во дворе стояли в ряд 3 большие клетки, окрашенные в разные цвета: красный, желтый и зеленый. В клетках жили кролики, причем в зеленой их было вдвое больше, чем в желтой. Однажды из левой клетки взяли 5 кроликов для живого уголка, а половину оставшихся перевели в красную клетку.
Вопрос:
Какого цвета была левая клетка?
Клетка была желтая. Задача подсказывает, что в зеленой клетке кроликов было вдвое больше — следовательно, их там четное количество. После того как из левой клетки забрали пятерых, в ней осталось тоже четное количество (так как легко разделилось пополам). Значит, до взятия количество кроликов было нечетным. Таким образом, левая клетка — не зеленая. Но и не красная, что видно из условия задачи.
6. Кто виноват?
Поздно вечером в одном из переулков неизвестная машина сбила человека и скрылась. Постовой милиционер обратил внимание, что автомобиль двигался с большой скоростью. 6 человек, оказавшихся неподалеку, сообщили противоречивые сведения.
Постовой милиционер обратил внимание, что автомобиль двигался с большой скоростью. 6 человек, оказавшихся неподалеку, сообщили противоречивые сведения.
Эти задачи можно решить с ходу, жуя бутерброд в обеденный перерыв. А можно сломать весь мозг, но так и не сообразить, где тут правда и в чем подвох.
1. Загадка о заключенных
4 заключенных приговорены к казни.
На них надели две белые шляпы и две черные шляпы. Мужчины не знают, какого цвета шляпы они носят. Четверых заключенных выстроили друг за другом (см. рисунок) таким образом, что:
Заключенный № 1 может видеть заключенных № 2 и № 3.
Заключенный № 2 может видеть заключенного № 3.
Заключенный № 3 не видит никого.
Заключенный № 4 не видит никого.
Судья любому заключенному, назвавшему цвет своей шляпы, пообещал свободу.
Вопрос:
Кто назвал цвет своей шляпы первым?
4-й и 3-й заключенные молчат, потому что вообще ничего не видят.
1-й заключенный молчит, потому что видит перед собой шляпы разного цвета: у 2-го и 3-го. Соответственно у него либо белая, либо черная шляпа.
Соответственно у него либо белая, либо черная шляпа.
2-й заключенный, понимая, что 1-й молчит, делает вывод о том, что у него шляпа не такого цвета, как у 3-го, а именно белого цвета.
Вывод:
Первым назвал цвет своей шляпы заключенный № 2.
2. Трудности на дороге
Один человек, меняя колесо у своей машины, уронил все 4 гайки крепления в решетку канализационного стока. Достать их оттуда невозможно. Водитель уже решил, что застрял на дороге надолго, но тут проходящий мимо ребенок посоветовал, как закрепить колесо. Водитель последовал совету и спокойно доехал до ближайшей шиномонтажки.
Вопрос:
Что посоветовал ребенок?
Отвернуть по 1 гайке от оставшихся 3 колес и закрепить ими 4-е.
3. Явка провалена
Человеку нужно было проникнуть в секретный клуб, не вызвав подозрений. Он заметил, что все приходящие сначала отвечали на вопросы охранника и лишь затем входили. Первому пришедшему был задан вопрос: «22?» Он ответил: «11!» — и прошел. Второму: «28?» Ответ был: «14». И тоже оказался верным. Человек решил, что все просто, и смело подошел к охраннику. «42?» — спросил охранник. «21!» — уверенно ответил человек и сразу же был изгнан.
Второму: «28?» Ответ был: «14». И тоже оказался верным. Человек решил, что все просто, и смело подошел к охраннику. «42?» — спросил охранник. «21!» — уверенно ответил человек и сразу же был изгнан.
Вопрос:
Почему?
На первый взгляд кажется, что пароль — это результат деления названного числа на 2. На самом деле это количество букв в предложенных числах. Верный ответ не 21, а 8.
4. Подарок Бабы-яги
Лето уже закончилось, когда Иван-царевич, направлявшийся в тридевятое царство за невестой, попросил ночлега в избушке на курьих ножках. Баба-яга ласково встретила гостя, напоила, накормила, спать уложила. На следующее утро она проводила Ивана-царевича с таким напутствием: «Встретится тебе по дороге река, моста через нее нет — придется тебе плыть. Возьми этот волшебный кафтан. Наденешь его — и бросайся смело в реку, кафтан не даст утонуть». Сто дней и ночей шел Иван-царевич и добрался наконец до реки. Но, чтобы преодолеть ее, кафтан ему не понадобился.
Вопрос:
Почему?
Иван-царевич был у Бабы-яги в сентябре. Отсчитываем 100 дней и узнаем, что зима уже в разгаре. Река скована льдом, и ее можно спокойно перейти и без кафтана.
Отсчитываем 100 дней и узнаем, что зима уже в разгаре. Река скована льдом, и ее можно спокойно перейти и без кафтана.
5. Клетки с кроликами
Во дворе стояли в ряд 3 большие клетки, окрашенные в разные цвета: красный, желтый и зеленый. В клетках жили кролики, причем в зеленой их было вдвое больше, чем в желтой. Однажды из левой клетки взяли 5 кроликов для живого уголка, а половину оставшихся перевели в красную клетку.
Вопрос:
Какого цвета была левая клетка?
Клетка была желтая. Задача подсказывает, что в зеленой клетке кроликов было вдвое больше — следовательно, их там четное количество. После того как из левой клетки забрали пятерых, в ней осталось тоже четное количество (так как легко разделилось пополам). Значит, до взятия количество кроликов было нечетным. Таким образом, левая клетка — не зеленая. Но и не красная, что видно из условия задачи.
6. Кто виноват?
Поздно вечером в одном из переулков неизвестная машина сбила человека и скрылась. Постовой милиционер обратил внимание, что автомобиль двигался с большой скоростью. 6 человек, оказавшихся неподалеку, сообщили противоречивые сведения:
Постовой милиционер обратил внимание, что автомобиль двигался с большой скоростью. 6 человек, оказавшихся неподалеку, сообщили противоречивые сведения:
- «Машина синего цвета, за рулем был мужчина».
- «Машина шла на большой скорости и с погашенными фарами».
- «Машина была с номерным знаком и шла не очень быстро».
- «Машина „Москвич“ шла с погашенным светом».
- «Машина без номерного знака, за рулем была женщина».
- «Машина „Победа“, серого цвета».
Когда задержали автомобиль, выяснилось, что лишь один свидетель сообщил верные сведения. Остальные пятеро — по одному правильному и одному неправильному факту.
Назовите
марку, цвет и скорость автомобиля. Имела ли машина номерной знак, шла ли она со светом и кто ее вел: мужчина или женщина?
Это была «Победа», синего цвета, с номерным знаком. Шла на большой скорости и с погашенными фарами. За рулем была женщина. Ориентируемся на показания постового — высокая скорость автомобиля. Зная, что свидетельство о низкой скорости заведомо неверное, определяем оставшиеся варианты.
Зная, что свидетельство о низкой скорости заведомо неверное, определяем оставшиеся варианты.
7. Бонус
Так что же делают одновременно все люди на Земле?
Становятся старше.
В тюрьме сидят 10 заключенных, каждый — в одиночной камере. Общаться между собой они не могут. В один прекрасный день начальник тюрьмы объявил им, что предоставляет всем шанс выйти на свободу на следующих условиях:
«В подвале тюрьмы есть комната с переключателем, имеющим два состояния: ON и OFF («вкл.» и «выкл.»). Каждую ночь я буду приводить в эту комнату ровно одного заключенного (выбирая его абсолютно случайно) и через некоторое время уводить. Находясь в комнате, каждый из вас может либо изменить положение переключателя, либо ничего с ним не делать. Персонал тюрьмы трогать этот переключатель не будет. В какой-то момент один из вас (любой) должен понять, что в комнате побывали все заключенные, и сообщить об этом. Если он окажется прав — всех отпустят, если ошибется — все вы навсегда останетесь в тюрьме. Я обещаю, что в комнате побывают все заключенные, причем каждого будут приводить туда неограниченное число раз
Я обещаю, что в комнате побывают все заключенные, причем каждого будут приводить туда неограниченное число раз
».
После этого заключенным разрешили собраться и обсудить стратегию действий, а потом развели обратно по камерам.
Могут ли
заключенные гарантированно выйти на свободу, и если да, то как
им этого добиться?
Подсказка
Казалось бы, как заключенный, которого привели в комнату, может воспользоваться тем, что видит переключатель в положении ON? И если он переключит его на OFF — как следующему заключенному воспользоваться этим?
Тем не менее стратегия, гарантированно приводящая узников к спасению, существует. Например, узники могут разбить дни на декады (10-дневные промежутки) и договориться, что дожидаются такого вот события: первого из них заведут в комнату в первый день декады, второго — во второй день и т. д., десятого — в последний день. Поскольку вероятность такого события отлична от нуля, то рано или поздно оно произойдет! Догадайтесь, как они могут действовать, чтобы 10-й смог понять,что такое событие в данной декаде на самом деле произошло.
Решение
1.
Самый простой, но и самый долгий вариант — действовать так, как было сказано в подсказке. Чтобы просигнализировать последнему, каждый из заключенных, которого завели в комнату НЕ В СВОЙ день, должен поставить переключатель в положение ON. Если же 10-й заключенный действительно оказался в комнате на 10-й день декады и видит переключатель в положении OFF, он немедленно говорит начальнику тюрьмы, что в комнате побывали все заключенные. Если в 10-й день в комнате оказался кто-то другой или же 10-й видит переключатель в положении ON, то всё начинается заново…
Это решение, несмотря на всю свою простоту, плохо в главном — бедным узникам придется слишком долго ждать. Действительно, из всех возможных 10 10 вариантов посещения ими комнаты в течение декады их устраивает только один — таким образом, вероятность p
их выхода на волю в течение одной декады равна 1/10 10 . Сравнительно несложными вычислениями можно доказать, что среднее время, которое потребуется им на освобождение, равно 1/p
= 10 10 декад, или 10 11 дней, или более 270 миллионов лет. В общем, столько люди не живут.
В общем, столько люди не живут.
2.
Однако это же решение подсказывает, как они могут ускорить свой выход на свободу. Для этого они должны дожидаться следующего события: в течение декады каждый из 10 человек побывал в комнате ровно один раз. Как такое событие «сигнализируется»? Да почти так же: если кого-нибудь заводят второй раз в одной декаде, он ставит переключатель на ON. Таким образом, если на 10-й день декады узник, которого туда отвели, оказался там впервые (за декаду) и видит переключатель в положении OFF, он сообщает начальнику тюрьмы, что всех можно освобождать.
Этот способ работает уже существенно быстрее, потому что количество благоприятных исходов теперь не 1, а 10! = 3628800. Это означает, что вероятность p»
выхода на свободу за первую же декаду не так уж и мала — она равна 0,00036288. Следовательно, ожидаемое число декад до выхода равно 1/p»
≈ 2755, то есть освободятся они примерно через 75 лет. Так что кто-нибудь, может быть, и доживет до освобождения, хотя особо надеяться на это не стоит.
Неужели всё так печально?
3.
К счастью, у заключенных существует принципиально другой способ действий.
Например,они могут договориться о том, что тот, кого заведут в комнату в первую ночь, выставляет переключатель на OFF и становится СЧЕТЧИКОМ. Остальные заключенные остаются ОБЫЧНЫМИ. Каждый обычный заключенный должен передать счетчику ровно один сигнал о своем попадании в комнату с переключателем. Это делается так: попав туда, обычный заключенный смотрит на положение переключателя. Если оно OFF, то заключенный ставит его на ON и считает сигнал переданным. Если же выключатель уже находится в положении ON, то заключенный ничего не делает — иначе говоря, ждет следующего подходящего случая.
Счетчик, попадая в камеру и видя переключатель в положении ON, понимает, что ему передали сигнал (запоминает это), а чтобы сделать возможной передачу следующего сигнала — ставит переключатель в OFF. Если же он видит переключатель в OFF, то ничего не делает и тоже ждет следующего раза.
Как только счетчик примет 9-й сигнал, он сразу же сообщает об этом начальнику тюрьмы.
Как долго продлится их отсидка при такой стратегии? Сосчитать это уже не столь просто, как раньше, потому что вероятность того, что заключенному в очередной день удастся передать сигнал, постепенно уменьшается от 9/10 для первого сигнала до 1/10 для последнего сигнала. В то же время вероятность попадания в комнату Счетчика в любой момент равна 1/10. Тем не менее механизм подсчета в целом аналогичен: до момента передачи первого сигнала в среднем пройдет 10/9 дня, а до момента его приема Счетчиком — еще 10 дней. Затем на второй сигнал уйдет 10/8 + 10 дней, на третий — 10/7 + 10, и так далее. Итого дней — совсем не так много, как в предыдущих решениях.
Послесловие
А не существует ли еще более быстрой стратегии действий?
Для 10 заключенных, возможно, и нет, а вот для большего количества — есть. Автор этой стратегии Б. Фельгенауэр назвал ее «пирамидальной».
Чтобы ее было проще понять, давайте будем считать,что количество заключенных равно степени двойки, например 64. Как и в предыдущем решении, каждый должен либо отдать сигнал (ровно один), либо собрать все сигналы. Для того чтобы им было сподручнее это делать, все ночи разбиты на участки разной «стоимости»: сначала идут «1-ночи», в течение которых все отдают либо принимают одинарные сигналы, затем идут «2-ночи», в течение которых все отдают либо принимают «двойные» сигналы, то есть каждый сигнал сообщает о двоих заключенных, затем наступают «4-ночи», «8-ночи», и т. д. Если всё происходит успешно, то когда дело доходит до «32-ночей», носителями сигналов остаются ровно двое заключенных, и в течение 32-ночей один из них отдает свой сигнал другому, после чего тот понимает, что собрал коллекцию из всех 64 сигналов, и значит, в комнате побывали все.
Как и в предыдущем решении, каждый должен либо отдать сигнал (ровно один), либо собрать все сигналы. Для того чтобы им было сподручнее это делать, все ночи разбиты на участки разной «стоимости»: сначала идут «1-ночи», в течение которых все отдают либо принимают одинарные сигналы, затем идут «2-ночи», в течение которых все отдают либо принимают «двойные» сигналы, то есть каждый сигнал сообщает о двоих заключенных, затем наступают «4-ночи», «8-ночи», и т. д. Если всё происходит успешно, то когда дело доходит до «32-ночей», носителями сигналов остаются ровно двое заключенных, и в течение 32-ночей один из них отдает свой сигнал другому, после чего тот понимает, что собрал коллекцию из всех 64 сигналов, и значит, в комнате побывали все.
Разумеется, такая «успешность» может и не случиться, поэтому после 32-ночей весь цикл 1-, 2-, 4-, 8-, 16-, 32-ночей повторяется сначала.
Как же происходит отдача и прием сигналов в пирамидальной схеме?
А вот как: если во время k
-ночи заключенный пришел в комнату и видит переключатель в положении ON, то он принимает k
-сигнал и ставит переключатель в OFF. Если к этому моменту у него уже был один k
Если к этому моменту у него уже был один k
-сигнал, то теперь у него есть два таких сигнала, или один 2k
-сигнал (который он попытается либо отдать, либо снова удвоить в период 2k
-ночей). Если же он пришел в комнату со своим k
-сигналом и видит OFF, то он ставит ON и считает k
-сигнал отданным.
Вот, в целом, и всё. Остальное уже является занудными техническими подробностями (какова должна быть продолжительность ночей определенного типа для того, чтобы передача всех нужных сигналов состоялась с достаточной вероятностью, и при этом не было слишком большой задержки перед наступлением следующего типа ночей).
Эта задача имеет самое прямое отношение к теории информации — она демонстрирует, что даже самый узкий (всего 1 бит — ON/OFF) канал позволяет передать достаточно много информации.
Кто именно является автором «тюремной» формулировки, мне неизвестно, но именно эта забавная формулировка буквально покорила мир. Кроме того, несмотря на относительную молодость задачи, она уже успела обрасти кучей самых неожиданных вариаций и усложнений. Например:
Например:
Два переключателя.
В комнате, куда приводят заключенных, не один, а целых два переключателя (следовательно, выйти на свободу можно быстрее. Вопрос: насколько?)
Две комнаты.
Заключенных водят не в одну, а в две разных комнаты, выбирая их также случайным образом. В каждой комнате — свой переключатель.
Разделение передатчика и приемника
. Каждую полночь начальник тюрьмы ставит переключатель в положение OFF. В час ночи он приводит туда первого заключенного, потом уводит, а в два часа ночи приводит туда же второго. Таким образом, первый из них должен «сработать» передатчиком информации, а второй — приемником.
Злобный начальник
. Начальник тюрьмы знает стратегию узников и каждый день выбирает для посещения комнаты такого заключенного, чтобы максимально затруднить узникам их задачу.
1. Загадка о заключенных
4 заключенных приговорены к казни
На них надели две белые шляпы и две черные шляпы. Мужчины не знают, какого цвета шляпы они носят. Четверых заключенных выстроили друг за другом (см. рисунок) таким образом, что:
Четверых заключенных выстроили друг за другом (см. рисунок) таким образом, что:
Заключенный № 1 может видеть заключенных № 2 и № 3.
Заключенный № 2 может видеть заключенного № 3.
Заключенный № 3 не видит никого.
Заключенный № 4 не видит никого.
Судья любому заключенному, назвавшему цвет своей шляпы, пообещал свободу.
Вопрос:
Кто назвал цвет своей шляпы первым?
2. Трудности на дороге
Один человек, меняя колесо у своей машины, уронил все 4 гайки крепления в решетку канализационного стока. Достать их оттуда невозможно. Водитель уже решил, что застрял на дороге надолго, но тут проходящий мимо ребенок посоветовал, как закрепить колесо. Водитель последовал совету и спокойно доехал до ближайшей шиномонтажки.
Вопрос:
Что посоветовал ребенок?
3. Явка провалена
Человеку нужно было проникнуть в секретный клуб, не вызвав подозрений. Он заметил, что все приходящие сначала отвечали на вопросы охранника и лишь затем входили. Первому пришедшему был задан вопрос: «22?» Он ответил: «11!» — и прошел. Второму: «28?» Ответ был: «14». И тоже оказался верным. Человек решил, что все просто, и смело подошел к охраннику. «42?» — спросил охранник. «21!» — уверенно ответил человек и сразу же был изгнан.
Первому пришедшему был задан вопрос: «22?» Он ответил: «11!» — и прошел. Второму: «28?» Ответ был: «14». И тоже оказался верным. Человек решил, что все просто, и смело подошел к охраннику. «42?» — спросил охранник. «21!» — уверенно ответил человек и сразу же был изгнан.
Вопрос:
Почему?
4. Подарок Бабы-яги
Лето уже закончилось, когда Иван-царевич, направлявшийся в тридевятое царство за невестой, попросил ночлега в избушке на курьих ножках. Баба-яга ласково встретила гостя, напоила, накормила, спать уложила. На следующее утро она проводила Ивана-царевича с таким напутствием: «Встретится тебе по дороге река, моста через нее нет — придется тебе плыть. Возьми этот волшебный кафтан. Наденешь его — и бросайся смело в реку, кафтан не даст утонуть». Сто дней и ночей шел Иван-царевич и добрался наконец до реки. Но, чтобы преодолеть ее, кафтан ему не понадобился.
Вопрос:
Почему?
5. Клетки с кроликами
Во дворе стояли в ряд 3 большие клетки, окрашенные в разные цвета: красный, желтый и зеленый. В клетках жили кролики, причем в зеленой их было вдвое больше, чем в желтой. Однажды из левой клетки взяли 5 кроликов для живого уголка, а половину оставшихся перевели в красную клетку.
В клетках жили кролики, причем в зеленой их было вдвое больше, чем в желтой. Однажды из левой клетки взяли 5 кроликов для живого уголка, а половину оставшихся перевели в красную клетку.
Вопрос:
Какого цвета была левая клетка?
6. Кто виноват?
Поздно вечером в одном из переулков неизвестная машина сбила человека и скрылась. Постовой милиционер обратил внимание, что автомобиль двигался с большой скоростью. 6 человек, оказавшихся неподалеку, сообщили противоречивые сведения: «Машина синего цвета, за рулем был мужчина».«Машина шла на большой скорости и с погашенными фарами». «Машина была с номерным знаком и шла не очень быстро». «Машина „Москвич“ шла с погашенным светом». «Машина без номерного знака, за рулем была женщина».«Машина „Победа“, серого цвета».
Когда задержали автомобиль, выяснилось, что лишь один свидетель сообщил верные сведения. Остальные пятеро — по одному правильному и одному неправильному факту.
Назовите
марку, цвет и скорость автомобиля. Имела ли машина номерной знак, шла ли она со светом и кто ее вел: мужчина или женщина?
Имела ли машина номерной знак, шла ли она со светом и кто ее вел: мужчина или женщина?
7. Бонус
Так что же делают одновременно все люди на Земле?
Ответы:
- 4-й и 3-й заключенные молчат, потому что вообще ничего не видят. 1-й заключенный молчит, потому что видит перед собой шляпы разного цвета: у 2-го и 3-го. Соответственно у него либо белая, либо черная шляпа. 2-й заключенный, понимая, что 1-й молчит, делает вывод о том, что у него шляпа не такого цвета, как у 3-го, а именно белого цвета. Вывод:
Первым назвал цвет своей шляпы заключенный № 2. - Отвернуть по 1 гайке от оставшихся 3 колес и закрепить ими 4-е.
- На первый взгляд кажется, что пароль — это результат деления названного числа на 2. На самом деле это количество букв в предложенных числах. Верный ответ не 21, а 8.
- Иван-царевич был у Бабы-яги в сентябре. Отсчитываем 100 дней и узнаем, что зима уже в разгаре. Река скована льдом, и ее можно спокойно перейти и без кафтана.

- Клетка была желтая. Задача подсказывает, что в зеленой клетке кроликов было вдвое больше — следовательно, их там четное количество. После того как из левой клетки забрали пятерых, в ней осталось тоже четное количество (так как легко разделилось пополам). Значит, до взятия количество кроликов было нечетным. Таким образом, левая клетка — не зеленая. Но и не красная, что видно из условия задачи.
- Это была «Победа», синего цвета, с номерным знаком. Шла на большой скорости и с погашенными фарами. За рулем была женщина. Ориентируемся на показания постового — высокая скорость автомобиля. Зная, что свидетельство о низкой скорости заведомо неверное, определяем оставшиеся варианты.
- Становятся старше.
По материалам Smekalka
Заключенные и шляпы
Пожертвуйте свой автомобиль в три простых шага
Пожертвовать свой автомобиль можно просто и быстро с помощью самой надежной программы пожертвований автомобилей Общественного радио.

Расскажите о себе и своей машине
Забираем и продаем
Преимущества вашей станции
- Дом
- Головоломки
- Заключенные и шляпы
26 декабря 2020 г.
РЭЙ: Начальник впускает троих заключенных в свои камеры. Он говорит им: «У одного из вас, ребята, будет шанс выбраться. Вот договор: я собираюсь завязать глаза всем вам, а затем надену шляпы на ваши головы. У меня есть три белых шляпы и две черные шляпы. Каждый из вас получит шляпу. Вы должны выяснить, какой цвет шляпы вы должны получить».
Он завязывает им глаза и надевает шляпу на каждого заключенного. Их выводят из комнаты гуськом. Когда с глаз сняты повязки, парень сзади может видеть двух человек перед собой, парень посередине может видеть одного парня перед собой, а парень впереди никого не видит.
Они не могут развернуться и должны ходить по тюрьме в таком порядке. И они ходят по тюрьме, останавливаясь у кабинета надзирателя. Надзиратель говорит парню сзади, который может видеть двух человек перед собой и их шляпы: «Можете ли вы сказать мне, какого цвета ваша шляпа?
Не забывайте, есть три белых и две черных шляпы. Парень сзади ничего не говорит. Он не знает.
Парню в середине задают тот же вопрос. Он не может ответить.
Парень впереди, который не видит шляп, знает. Он говорит: «Я могу определить цвет своей шляпы».
Откуда он знает?
Ответ:
РЭЙ: Его шляпа была белой. Он знал, потому что двое других парней не знали, какого цвета шляпы на каждом из них. Поскольку задний заключенный ничего не сказал, он, должно быть, видел перед собой либо две белые шляпы, либо черно-белую шляпу.
Теперь, если бы заключенный в середине увидел перед собой черную шляпу, он бы знал, что на нем белая шляпа. Почему это? Потому что если бы на нем была черная шляпа, то парень, который был сзади, знал бы, что его собственная шляпа белая, и заговорил бы, когда у него был шанс.
Почему это? Потому что если бы на нем была черная шляпа, то парень, который был сзади, знал бы, что его собственная шляпа белая, и заговорил бы, когда у него был шанс.
Поскольку заключенный сзади и посередине ничего не сказал, заключенный впереди знал, что у него белая шляпа.
Получайте еженедельную электронную почту Puzzler
Архив Головоломок
Получить информационный бюллетень Car Talk
Блоги
Блоги
Блоги
Самое странное следствие аксиомы выбора — возрастающая энтропия
Этот пост посвящен самой поразительной головоломке, которую я когда-либо слышал. Во-первых, две головоломки для разминки.
Четверо заключенных, две черные шляпы, две белые шляпы
Четыре заключенных стоят в шеренгу, причем самый передний спрятан от остальных за стеной. На каждом шляпа, но они не видят ее цвета. Есть две черные шляпы и две белые шляпы, и все четверо это знают.
На каждом шляпа, но они не видят ее цвета. Есть две черные шляпы и две белые шляпы, и все четверо это знают.
Как только любой заключенный узнает цвет своей шляпы, он должен объявить об этом. Если они правы, все уходят на свободу. Они не могут разговаривать друг с другом или смотреть в любом направлении, кроме как вперед.
Им гарантирована свобода?
Решение
Да, они есть! Если D увидит шапку одного цвета на головах B и C, то он может сделать вывод, что цвет его шапки другого цвета, поэтому все выходят на свободу. Если он видит разноцветные шапки, то не может сделать вывод о цвете своей шапки. Но C это знает, поэтому, если D не объявляет цвет своей шляпы, то C знает, что цвет его шляпы отличается от цвета шляпы B, и все они освобождаются. Сделанный!
Следующий:
Десять заключенных, неизвестное количество черных и белых шляп
Каждому заключенному случайным образом назначается головной убор. Количество черных и белых шляп неизвестно. Начиная со спины, каждый должен угадать цвет своей шляпы. Если они совпадают, их отпускают, а если нет, то убивают на месте. Они могут координировать свои действия заранее, но не могут обмениваться информацией после того, как процесс начался.
Начиная со спины, каждый должен угадать цвет своей шляпы. Если они совпадают, их отпускают, а если нет, то убивают на месте. Они могут координировать свои действия заранее, но не могут обмениваться информацией после того, как процесс начался.
Есть стратегия, которая дает девяти заключенным 100% шанс на выживание, а другому 50%. Что это такое?
Раствор
A 10 считает количество белых шляп перед собой. Если это нечетно, он говорит «белый». В противном случае он говорит «черный». Это позволяет каждому заключенному узнать свой собственный цвет шляпы, как только он услышит заключенного позади себя.
— — —
Хорошо, теперь, когда вы все размялись, давайте немного усложним задачу.
Бесчисленное количество заключенных, неизвестное количество черных и белых шляп, отсутствие слуха
Бесчисленное количество заключенных, выстроенных в ряд со случайно назначенными шляпами. Каждый из них знает свое место в очереди.
Угадывание шляпы начинается с A 1 в конце очереди. Те же последствия, что и раньше: награда за правильное предположение — свобода, а наказание за неправильное предположение — смерть.
Те же последствия, что и раньше: награда за правильное предположение — свобода, а наказание за неправильное предположение — смерть.
У заключенных была возможность встретиться и обсудить план заранее, но теперь все они глухие. Они не только не могут скоординироваться, когда начинается угадывание, но и понятия не имеют, что произошло позади них в очереди.
Загадка для вас: можете ли вы найти стратегию, которая гарантирует, что только конечное число заключенных будет убито?
О боже, заключенным здесь очень тяжело. Мы протянем им руку помощи; давайте дадим им логическое всеведение и способность запоминать неисчислимую бесконечность информации. Черт возьми, давайте также дадим им оракул для вычисления любой функции, которая им нравится.
Попробуйте!
(…)
(…)
Решение
Удивительно, но ответ положительный. Все заключенные, кроме конечного числа, могут быть спасены.
Вот стратегия. Сначала начнем с идентификации белых шляп с номером 0 и черных шляп с номером 1. Теперь набор всех возможных последовательностей шляп в строке представляет собой набор всех двоичных последовательностей. Мы определяем отношение эквивалентности для таких последовательностей следующим образом: 𝑥 ~ 𝑦 тогда и только тогда, когда 𝑥 и 𝑦 идентичны после конечного числа цифр в последовательности. Это разделит все возможные последовательности на классы эквивалентности.
Теперь набор всех возможных последовательностей шляп в строке представляет собой набор всех двоичных последовательностей. Мы определяем отношение эквивалентности для таких последовательностей следующим образом: 𝑥 ~ 𝑦 тогда и только тогда, когда 𝑥 и 𝑦 идентичны после конечного числа цифр в последовательности. Это разделит все возможные последовательности на классы эквивалентности.
Например, класс эквивалентности 0 будет просто подмножеством рациональных чисел, бинарное расширение которых заканчивается в некоторой точке (т. е. подмножество рациональных чисел, которое может быть записано как целое число в степени двойки). Почему? Что ж, если двоичная последовательность 𝑥 эквивалентна .000000…, то после конечного числа цифр 𝑥 она должна будет всегда состоять из 0. А это значит, что его можно записать в виде некоторого целого числа в степени 2.
Когда заключенные встречаются заранее, они используют аксиому выбора, чтобы выбрать одного представителя из каждого класса эквивалентности. (Небольшое напоминание: аксиома выбора гласит, что из любого множества 𝑥 непустых непересекающихся множеств можно составить новое множество, которое имеет ровно один общий элемент с каждым из множеств в 𝑥.) Теперь каждый заключенный держит в голове несчетное множество последовательностей, каждая из которых представляет класс эквивалентности.
(Небольшое напоминание: аксиома выбора гласит, что из любого множества 𝑥 непустых непересекающихся множеств можно составить новое множество, которое имеет ровно один общий элемент с каждым из множеств в 𝑥.) Теперь каждый заключенный держит в голове несчетное множество последовательностей, каждая из которых представляет класс эквивалентности.
Оказавшись в комнате, каждый заключенный может видеть все шляпы, кроме конечного числа, и поэтому он точно знает, к какому классу эквивалентности принадлежит последовательность шляп. Таким образом, каждый заключенный угадывает цвет своей шляпы, как если бы он был в репрезентативной последовательности из соответствующего класса эквивалентности. Поскольку фактическая последовательность и репрезентативная последовательность различаются только в конечном числе мест (все в начале), все записи будут одинаковыми после некоторого конечного числа заключенных. Так каждый заключенный после этой первой конечной партии будет спасен !
Этот результат настолько смехотворен, что я просто схожу с ума, думая об этом.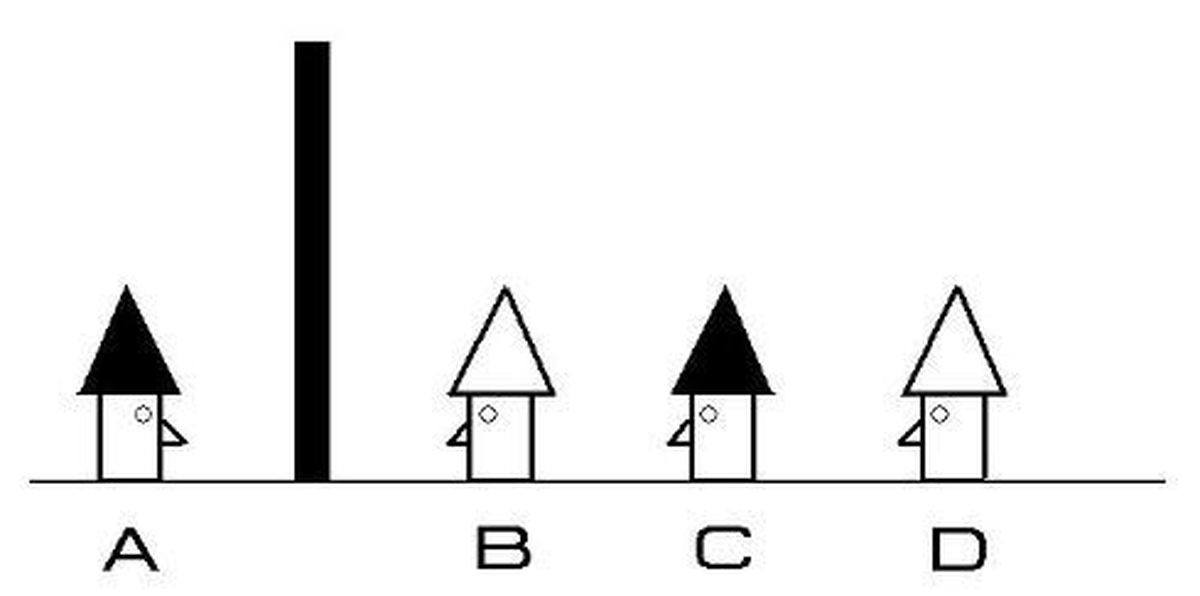 Наверняка здесь творится какая-то черная магия. Помните, что каждый заключенный может видеть все находящиеся перед ним шляпы, но они ничего не знают об общем количестве шляп каждого цвета, поэтому существует нет корреляции между шляпами, которые они видят, и шляпой на их голове. Более того, они глухие! Так что они не могут учиться любую новую информацию о том, что происходит за ними! У них буквально нет информации о цвете собственной шляпы. Таким образом, лучшее, что может сделать каждый человек, должно быть 50/50. Наверняка наверняка , это значит что смертей будет бесконечное количество.
Наверняка здесь творится какая-то черная магия. Помните, что каждый заключенный может видеть все находящиеся перед ним шляпы, но они ничего не знают об общем количестве шляп каждого цвета, поэтому существует нет корреляции между шляпами, которые они видят, и шляпой на их голове. Более того, они глухие! Так что они не могут учиться любую новую информацию о том, что происходит за ними! У них буквально нет информации о цвете собственной шляпы. Таким образом, лучшее, что может сделать каждый человек, должно быть 50/50. Наверняка наверняка , это значит что смертей будет бесконечное количество.
Но нет! Нет, если вы принимаете аксиому выбора! Вам гарантировано только конечное число смертей, просто конечное число, которое может быть сколь угодно большим. Как это не противоречие? Что ж, чтобы это было противоречием, должно существовать некоторое распределение вероятностей возможных исходов, которое говорит, что Pr(конечное количество смертей) = 0. И оказывается, что набор репрезентативных последовательностей образует неизмеримое множество (множество, которое не может иметь четко определенный размер с использованием обычной меры Лебега). Таким образом, ему не может быть присвоена никакая вероятность (, а не нулевая вероятность, буквально неопределенная)! Теперь вспомните, что нулевая смертность происходит именно тогда, когда реальная последовательность является одной из репрезентативных последовательностей. Это означает, что этому положению вещей нельзя приписать вероятность. То же самое относится и к положению вещей, при котором умирает один арестант, или два арестанта и т.д. Вы буквально не можете определить распределение вероятностей по количеству заключенных, которые должны умереть.
Таким образом, ему не может быть присвоена никакая вероятность (, а не нулевая вероятность, буквально неопределенная)! Теперь вспомните, что нулевая смертность происходит именно тогда, когда реальная последовательность является одной из репрезентативных последовательностей. Это означает, что этому положению вещей нельзя приписать вероятность. То же самое относится и к положению вещей, при котором умирает один арестант, или два арестанта и т.д. Вы буквально не можете определить распределение вероятностей по количеству заключенных, которые должны умереть.
Кстати, а что будет, если у вас будет несчетная бесконечность заключенных? Скажем, мы делаем их бесконечно тонкими, а затем сжимаем их вдоль реальной линии, чтобы заполнить каждую точку. Каждый заключенный может видеть все головные уборы другого заключенного, кроме конечного числа. Давайте даже подарим им шляпы, имеющие несчетное количество разных цветов. Может быть, мы выбираем каждый цвет шляпы, просто случайным образом выбирая любую частоту видимого света.
Оказывается, мы все еще можем использовать аксиому выбора, чтобы гарантировать выживание всех заключенных, кроме конечного числа!
Реакция Кольбера, когда он впервые узнал о неисчисляемой версии задачи о шляпе
И последняя.
Бесчисленное количество заключенных, неизвестное количество черных и белых шляп, со слухом
У нас снова бесчисленное множество заключенных, каждый в черной или белой шляпе, но на этот раз они могут слышать цвета, вызываемые предыдущими заключенными. Теперь, насколько хорошо они могут сделать?
Ответ? (Предполагая аксиому выбора) Каждый заключенный может быть гарантировал выживание , за исключением первого, который выживает с вероятностью 50%. Я действительно хочу, чтобы это дошло до меня. Когда у нас было десять заключенных с десятью головными уборами, они могли провернуть это, используя свое знание общего количества черных и белых шляп среди них. У наших заключенных такого больше нет! Они начинают ничего не зная о количестве белых и черных шляп, кроме того, что они могут видеть перед собой. И тем не менее они все равно выходят из него со всеми, кроме одного заключенного, гарантированной свободой.
И тем не менее они все равно выходят из него со всеми, кроме одного заключенного, гарантированной свободой.
Как они это делают? Они начинаются так же, как и раньше, определяя отношение эквивалентности и выбирая репрезентативную последовательность из каждого класса эквивалентности. Теперь они помечают каждую отдельную последовательность либо 0, либо 1. Последовательность получает 0, если она отличается от репрезентативной последовательности в своем классе эквивалентности четным числом позиций, в противном случае она получает 1. Такая маркировка приводит к тому, что любые две последовательности, отличающиеся ровно на одну цифру, имеют противоположные метки.
Теперь первый человек (А) просто называет метку последовательности, которую он видит. Для следующего человека (B) это последовательность, которая начинается со шляпы. И помните, они знают, к какому классу эквивалентности они относятся, поскольку могут видеть всех, кто находится перед ними! Поэтому все, что им нужно сделать, это подумать, какой была бы метка последовательности, начинающейся с них, если бы они были в белой шляпе.


 Зная, что свидетельство о низкой скорости заведомо неверное, определяем оставшиеся варианты.
Зная, что свидетельство о низкой скорости заведомо неверное, определяем оставшиеся варианты.