Рассчитать не точно: Как пишется слово: «рассчитать неточно» или «рассчитать не точно»?
Как точно рассчитать количество кирпича и газобетона на дом?
Как часто, покупая материалы для строительства и ремонта, приходилось ошибаться с количеством? Сколько не пригодившихся рулонов обоев и банок с краской валяется сейчас по кладовкам россиян? Сколько досок гниет по сараям? Для большинства из нас это лишь мелочи жизни. Но если речь идет о более крупном и дорогом продукте, например, газобетон и кирпич, для хранения которых трудно выделить подходящую площадь, задумываются, что делать с остатками, уже практически все. Хорошо, если найдется покупатель, который заберет их со скидкой. Но так везет лишь немногим. Да и «скидки» – это денежные потери для Вашей собственной стройки.
Вот почему так важно уметь рассчитывать, как можно точнее, объем необходимых стройматериалов. В данном процессе должно быть учтено большое количество факторов и значений: габариты постройки, строительных элементов, наличие оконных и дверных проемов, фронтонов, карнизов, перекрытий, толщину раствора и конфигурацию кровли (для расчета кровельных и пиломатериалов) и т.д. Даже если покупатель разбирается в формулах для расчета, все же быстрее, удобнее и с защитой от человеческих ошибок, при вычислении, просто подставить конкретные значения и получить результат.
На сайте БлокСПб появилась практичное новшество для покупателей. Теперь, перед покупкой строительного материала, не придется высчитывать нужный объем самостоятельно, раз за разом перепроверяя себя, пересчитывать заново для каждого варианта товаров от разных производителей. Просто выбирайте нужное значение из выпадающего меню, впишите индивидуальные параметры постройки и узнайте необходимый объем сразу!
Мы продолжаем разработку строительных калькуляторов, и в ближайшее время на сайте появится возможность расчета кровельных и фасадных материалов, пиломатериалов и др. Все, чтобы Вы могли строить экономично! Сегодня и всегда.
Все, чтобы Вы могли строить экономично! Сегодня и всегда.
Следите за обновлениями БлокСПб!
Чек-лист, чтобы рассчитать налоги без проблем ― СБИС
Чек-лист, чтобы рассчитать налоги без проблем ― СБИС Используя официальный сайт sbis.ru, вы даете согласие на работу с cookie, Яндекс.Метрикой, Google Analytics для сбора технических данных. Подробнее
- 77 Москва
- 78 Санкт-Петербург
- 01 Республика Адыгея
- 02 Республика Башкортостан
- 03 Республика Бурятия
- 04 Республика Алтай
- 05 Республика Дагестан
- 06 Республика Ингушетия
- 07 Респ. Кабардино-Балкария
- 08 Республика Калмыкия
- 09 Респ. Карачаево-Черкессия
- 10 Республика Карелия
- 11 Республика Коми
- 12 Республика Марий Эл
- 13 Республика Мордовия
- 14 Республика Саха (Якутия)
- 15 Северная Осетия — Алания
- 16 Республика Татарстан
- 17 Республика Тыва
- 18 Республика Удмуртия
- 19 Республика Хакасия
- 20 Республика Чечня
- 21 Республика Чувашия
- 22 Алтайский край
- 23 Краснодарский край
- 24 Красноярский край
- 25 Приморский край
- 26 Ставропольский край
- 27 Хабаровский край
- 28 Амурская обл.
- 29 Архангельская обл.
- 30 Астраханская обл.
- 31 Белгородская обл.
- 32 Брянская обл.
- 33 Владимирская обл.
- 34 Волгоградская обл.

- 35 Вологодская обл.
- 36 Воронежская обл.
- 37 Ивановская обл.
- 38 Иркутская обл.
- 39 Калининградская обл.
- 40 Калужская обл.
- 41 Камчатский край
- 42 Кемеровская обл.
- 43 Кировская обл.
- 44 Костромская обл.
- 45 Курганская обл.
- 46 Курская обл.
- 47 Ленинградская обл.
- 48 Липецкая обл.
- 49 Магаданская обл.
- 50 Московская обл.
- 51 Мурманская обл.
- 52 Нижегородская обл.
- 53 Новгородская обл.
- 54 Новосибирская обл.
- 55 Омская обл.
- 56 Оренбургская обл.
- 57 Орловская обл.
- 58 Пензенская обл.
- 59 Пермский край
- 60 Псковская обл.
- 61 Ростовская обл.
- 62 Рязанская обл.
- 63 Самарская обл.
- 63 Тольятти
- 64 Саратовская обл.
- 65 Сахалинская обл.
- 66 Свердловская обл.
- 67 Смоленская обл.
- 68 Тамбовская обл.
- 69 Тверская обл.
- 70 Томская обл.
- 71 Тульская обл.
- 72 Тюменская обл.
- 73 Ульяновская обл.
- 74 Челябинская обл.
- 75 Забайкальский край
- 76 Ярославская обл.
- 79 Еврейская АО
- 83 Ненецкий АО
- 86 Ханты-Мансийский АО
- 87 Чукотский АО
- 89 Ямало-Ненецкий АО
- 91 Республика Крым
- 92 Севастополь
Как рассчитать вес фасада из ДСП и МДФ?
Для обеспечения максимального комфорта при приготовлении еды и работе на кухне крайне важно качество движения при открывании и закрывании фасадов. Оно, в свою очередь, обеспечивается грамотно подобранной и установленной фурнитурой.
Оно, в свою очередь, обеспечивается грамотно подобранной и установленной фурнитурой.
Чтобы грамотно подобрать подъемные механизмы или определить количество необходимых петель, необходимо максимально точно знать фес фасада или дверцы. Но, к сожалению, далеко не всегда это заветное значение точно знает даже производитель мебели.
Самый надежный и наиболее точный способ определения веса фасада – это взвесить фасад на домашних или иных весах, но это не всегда приемлемо. Для таких случаев расчет веса фасада производится по формуле:
FG = FH x FB x FD x Плотность, где:
- FG – вес фасада в килограммах;
- FH – высота фасада в метрах;
- FB – ширина фасада в метрах;
- FD – толщина фасада в метрах;
- Плотность – плотность материала, из которого изготовлен фасад в кг/м3.
Для расчета веса фасада из ДСП и МДФ значение плотности равно:
- 680 кг/м3 для ДСП;
- 760 кг/м3 для МДФ.
Обратите внимание, что данная формула определяет вес фасада без учета веса ручки. Для правильного подбора силового механизма необходимо учесть и вес ручки, а для подъемников серий HK, HK-S и HK-XS необходимо взять двойной вес ручки.
Для подбора комплектующих Blum, в полном каталоге в разделе «Информация» Вы можете найти таблицу значений ориентировочного веса фасада без ручки для фасадов из ДСП, МДФ и Алюминиевых рамок со стеклом стандартных размеров, толщиной 19 мм.
Вы можете скачать электронную версию каталога по ссылке и добавить к любому заказу в нашем интернет-магазине печатную версию каталога, совершенно бесплатно.
Как рассчитывается количество посещений точек?
Как рассчитывается количество посещений точек?
Начиная с 1 апреля 2021 г. оптимизация для посещений точек будет недоступна. Начиная с 1 мая 2021 г. метрика «Посещения точек» не будет показываться в отчетах по рекламе. Вы всё равно сможете создавать рекламу с целью «Посещаемость точек», используя оптимизацию для охвата или продаж в точках.
Вы всё равно сможете создавать рекламу с целью «Посещаемость точек», используя оптимизацию для охвата или продаж в точках.
Данные о посещениях точек
Посещения точек — это приблизительное количество посещений ваших точек в результате просмотра рекламы. Посещения обнаруживаются с помощью сводных данных, полученных от служб геолокации с использованием GPS, сигналов Bluetooth и Wi-Fi. Это приблизительная метрика, которая находится в разработке.
В отчетах по рекламе можно посмотреть данные о посещениях точек, которые произошли в течение 1, 7 и 28 дней после клика по объявлению или после его просмотра.
Так как не все посещения можно отследить, результаты метрики рассчитываются на основе статистического моделирования. Это значит, что они могут отражать неточное количество посещений и не связаны с определенными людьми. Например, если в них указано, что одну точку посетили 125 человек, это не значит, что все они пришли туда благодаря вашей рекламе. Это лишь приблизительное количество посещений, которое можно отнести к рекламе.
При анализе данных о посещениях точек помните следующее:
Поскольку посещения точек прогнозируются и моделируются, результаты этой метрики будут точнее, если точку посетят более 100 раз. Меньшее количество посещений позволяет получить некоторую информацию о разбивке результативности кампании. Но для общей оценки кампании нужно как можно больше посещений.
Поскольку мы отдельно оцениваем результаты на уровнях кампании, группы объявлений и отдельного объявления, количество посещений для кампании в Ads Manager может не соответствовать сумме посещений по ее компонентам. В первую очередь учитывайте результаты на уровне группы объявлений.
Посещения точек иногда определяются неточно. Например, если точка расположена в оживленном месте (на вокзале или в торговом центре), то понять, кто входил внутрь, а кто просто останавливался рядом, бывает непросто. Поэтому ради точности результатов количество посещений таких точек не учитывается.

- Если метка определенной точки на карте отличается от адреса, указанного в разделе Адреса точек, то результаты по ее посещениям также не будут входить в отчет или будут неправильными.
В метрике «Посещения точек» учитываются посещения только в тех странах, где вы имеете право проводить измерения. Если ваша кампания не таргетирована на такие страны, вы не увидите отчетность по посещениям точек.
Отчеты по посещениям могут быть получены и для точек, которые не входили в вашу группу точек, если люди, увидевшие рекламу одной точки, посетили другую.
Цена за посещение точки
Цена за посещение точки — это средняя стоимость каждого посещения точки. Это приблизительная метрика, которая находится в разработке.
Она рассчитывается как отношение общей суммы затрат на кампанию к количеству отнесенных к ней посещений. Цена кампании основана на количестве показов объявлений в ней. Цена за посещение точки не равна сумме затрат на посещение точки.
Статьи по теме
Купите ОСАГО онлайн с выгодой до 55%
Калькулятор ОСАГО 2021
Калькулятор ОСАГО – удобный инструмент, дающий собственникам автомобильного транспорта возможность узнать о цене приобретаемой автогражданки. Сервис предлагает не только ознакомиться с основными данными о страховании именно этой конторы, но также сравнить ценовую политику на рынке. Это позволит определить наиболее приемлемый вариант для оформления документа. Произвести расчеты стоимости ОСАГО калькулятор поможет не только для текущих клиентов компании, но также и тем, кто желает узнать больше о страховых предложениях, акциях и дисконтах.
Как рассчитать стоимость полиса ОСАГО
Чтобы получить данные о цене договора, следует основываться на базовой тарификации и коэффициентах, утвержденных законодательством РФ. Если коэффициент является постоянной величиной, то базовые тарифы устанавливает сама страховая компания. Это означает, что зависимо от выбранного страховщика могут меняться ставки на приобретение полиса. Рассчитать цену на ОСАГО поможет специальный калькулятор, при помощи которого вы быстро сможете узнать интересующие данные, а также доступных льготах.
Это означает, что зависимо от выбранного страховщика могут меняться ставки на приобретение полиса. Рассчитать цену на ОСАГО поможет специальный калькулятор, при помощи которого вы быстро сможете узнать интересующие данные, а также доступных льготах.
При подсчете вознаграждения страховщикам по свидетельству применяется формула, в которой берется номинальный тариф, а также следующие коэффициенты: мощности, ограничений, возраста и стажа, сезонности, территории и бонус-малус. Калькулятор ОСАГО в 2021 году производит расчет именно по этим значениям и дает понимание того, за что водитель платит при оформлении документа автогражданской ответственности. Важно указывать достоверную информацию, чтобы калькуляция произвелась максимально точно.
Чтобы рассчитать, сколько будет стоить страховка ОСАГО, в калькуляторе нужно указать следующее:
- данные о владельце и количестве водителей;
- тип транспорта;
- характеристики средства.
Как купить полис ОСАГО онлайн
Для удобства автолюбителей процедура оформления свидетельства значительно упростилась, и теперь подать заявку можно прямо на сайте организации. Чтобы это сделать, потребуется запомнить анкету, где вписать требуемую информацию о себе и ТС, на который оформляется договор. Также можно использовать калькулятор страховки ОСАГО 2021, чтобы подсчитать данные о стоимости обеспечения. С недавнего времени страхователь предлагает произвести процедуру расчета посредством официального портала. По завершению процесса оплаты вы получите уведомление на электронную почту с электронным полисом и другими важными данными. Следует помнить, что автогражданка начнет действовать только по истечению трехдневного периода.
Изменения в законодательстве
- Отмена коэффициента прицепа. Однако в номинальный тариф страховая компания может учесть эту величину.
- Индивидуальная тарификация.
 Страхователь имеет право установить индивидуальную ставку разным водителям, чьи средства передвижения были зарегистрированы на одной территории. При этом главной величиной в установлении тарификации является грубое нарушение ПДД.
Страхователь имеет право установить индивидуальную ставку разным водителям, чьи средства передвижения были зарегистрированы на одной территории. При этом главной величиной в установлении тарификации является грубое нарушение ПДД. - Показатели стажа. Водители со стажем будут платить меньше молодых.
- Региональные величины. Зависимо от местности, где было зарегистрировано авто, будет меняться КТ.
- Повысилась стоимость по коэффициенту ограниченного использования. Теперь он составляет 1.94.
- Расширение тарифных коридоров для всех видов транспорта.
Цены на автогражданку для легковых автомобилей претерпят изменений в Москве, Санкт-Петербурге и других регионах страны. Это связано с тем, что Центробанк пересмотрел действующие тарификации. Рассчитать страховку ОСАГО поможет калькулятор, где понадобиться указать подробную информацию о водителе и транспорте. Программа работает по специальной формуле подсчета, однако получить точную сумму оплаты у клиентов не получится в силу того, что нельзя узнать, какая базовая ставка будет применена к ним.
Страховые коэффициенты (КМ, КБМ)
Это важные величины, позволяющие произвести самостоятельные расчеты по ОСАГО на онлайн калькуляторе, и впоследствии оформить интересующий продукт. Основываясь на предоставленных данных, программа предложит оптимальную ставку с полагающимися преференциями. Для лиц, желающих оформить обеспечение, также важно учитывать, что тип автомобиля, место его регистрации и ряд других пунктов могут существенно повысить или понизить ставку.
Выделяются следующие значения:
- КМ – мощность транспорта, применяемая для авто легкового класса;
- КБМ – константа, понижающая или повышающая итоговую стоимость. На нее влияет фактор аварийности за предыдущие периоды;
- КТ – показатель территории регистрации средства передвижения;
- КО – пункт об ограниченном использовании.
 Равняется 1 в случае, если в договоре указаны определенные водители, если они не вписаны, стоимость страхования увеличивается вдове;
Равняется 1 в случае, если в договоре указаны определенные водители, если они не вписаны, стоимость страхования увеличивается вдове; - КВС – возраст и стаж собственника. Если одним автомобилем пользуется несколько водителей, принимает максимальное значение;
- КС – сезонность эксплуатации. Актуальна в случае, если договор оформляется не на годовой период, а несколько месяцев.
Порядок применения коэффициента «бонус-малус»
Используя калькулятор ОСАГО онлайн, автолюбитель имеет возможность узнать, сколько заплатит за страхование. Однако немаловажной величиной является класс КБМ – поощрение владельцев авто за вождение без ДТП, которое позволяет получить льготу, понижающую цену на полис вдвое. Если вы страхуетесь в первый раз, к вам будет применен коэффициент 1 и класс 3. В случае безаварийности по завершению действия договора сроком на один год, скидка на покупку очередного страхования составит 5%, а водительский класс повышается.
Значение КБМ также можно узнать на портале РСА. Если собственник прежде оформлял страхование и желает произвести повторную процедуру, эта величина будет определена в автоматическом порядке и применена в качестве полагаемого дисконта. Внесение достоверных данных поможет увидеть точные цифры по полагаемым преференциям. Перед заказом полиса ОСАГО на автомобиль используйте калькулятор, в котором можно увидеть итоговый дисконт по бонус-малус и другие полагающиеся льготы.
Заключение
Калькулятор страховки автомобиля от ОСАГО дает возможность получить информацию о приблизительной цене на приобретаемый полис. Подсчеты производятся с учетом тарифа и других важных показателей, влияющих на выплаты страхователю. Также собственник может воспользоваться порталом РСА, где размещены полезные материалы, касающиеся автогражданки и транспортного средства. Расчет цены на ОСАГО калькулятор производит в автоматическом режиме, достаточно указать требуемые сведения и получить интересующую информацию.
ОСАГО для марок автомобилей
ОСАГО для Тойоты
ОСАГО для Форда
ОСАГО для Хонды
ОСАГО для Ниссан
ОСАГО для Хундай
ОСАГО на Мерседес
ОСАГО для BMW
ОСАГО для Ауди
ОСАГО для Шкоды
ОСАГО для Лады
ОСАГО в страховых компаниях
ОСАГО Альфа
ОСАГО Росгосстрах
ОСАГО Ингосстрах
ОСАГО Тинькофф
ОСАГО Ресо
ОСАГО ВСК
ОСАГО СОГАЗ
ОСАГО Ренессанс
ОСАГО Согласие
ОСАГО в городах
ОСАГО в Москве
ОСАГО Санкт-Петербург
ОСАГО Екатеринбург
ОСАГО Нижний Новгород
ОСАГО Воронеж
ОСАГО Новосибирск
ОСАГО Уфа
ОСАГО Челябинск
ОСАГО Краснодар
ОСАГО Красноярск
ОСАГО Самара
ОСАГО Волгоград
ОСАГО Казань
ОСАГО Ростов-на-Дону
ОСАГО Пермь
ОСАГО Пенза
ОСАГО Омск
Калькулятор ЖД перевозок, рассчитать стоимость по России из Хабаровска ЖД транспортом
Калькулятор ж/д перевозок
Перед вами уникальный сервис, который поможет рассчитать предварительную стоимость отправления вашего груза компанией «Азимут» в другой город ж/д транспортом. Калькулятор ж/д перевозок – это отличный способ самостоятельно произвести расчет стоимости перевозки груза прямо сейчас.
Мы специально проработали все тонкости, чтобы конечная цифра в итоге была максимально приближена к той цене, которую вам озвучат при принятии груза к отправлению. В режиме онлайн вы получите стоимость отправления груза из Хабаровска в любой город России.
Как пользоваться калькулятором ж/д перевозок
Для того, чтобы получить предельно точный результат, требуется ввести все параметры калькулятора ж/д перевозок. Так, обязательными являются поля:
- город, откуда вы отправляете груз;
- пункт назначения;
- заполненное хотя бы одно поле из веса, объема или размеров груза.

Ряд дополнительных параметров поможет определить категорию груза, и рассчитать цену на перевозку более точно. Мы всегда бережно относимся к грузу, однако, если вы перевозите что-то хрупкое, мы настойчиво рекомендуем не пренебрегать дополнительной маркировкой. Данная характеристика груза также может отразиться и на конечной стоимости перевозки, поэтому при самостоятельном онлайн-расчете на калькуляторе ставьте галочку «Хрупкое» в этом случае.
Для крупногабаритного груза также действуют особые условия. Если у вас намечается доставка груза, вес одного места которого свыше 250 кг, или хотя бы одна сторона в упакованном состоянии превышает 3 м, он является негабаритным, это тоже может отразиться на цене. Для клиентов, которые заказывают транспортировку груза целыми вагонами, у нас есть специальные предложения и ощутимые скидки.
Калькулятор ж/д перевозок рассчитывает цену на транспортировку груза, исходя из тарифов, размещенных на нашем сайте.
рассчитать длину материала на забор Кенгуру.Советы
Не секрет, что сетка-рабица один из
самых излюбленных
материалов при возведении забора. Такие заграждения легко монтируются, хорошо пропускают солнечные лучи, имеют
относительно низкую рыночную стоимость и высокую степень экологичности. Кроме того, сетка-рабица абсолютно
универсальна. Так, если останется пара лишних метров, то они могут пойти на небольшой вольер для питомцев. Если
же вы хотите точно рассчитать материал для забора, не переплачивая за лишние сантиметры, мы поможем это сделать.
Расчет сетки-рабицы для забора: простые истины
Для начала необходимо определиться с исходными элементами: самим ограждением, креплением и опорными столбами. В
зависимости от опоры используются разные виды крепежа и способы расчета.
Выбирая деревянные брусья, необходимо знать периметр участка. Это позволит максимально точно определить размеры
сетки для ограждения. Так как рабица будет плотно прилегать к брусьям и крепиться с помощью саморезов и досок,
Так как рабица будет плотно прилегать к брусьям и крепиться с помощью саморезов и досок,
то ее
размеры полностью совпадут с периметром участка.
Тоже самое можно сказать и о расчете длины забора из рабицы c металлическим, асбестовым или бетонным
основанием,
при условии, если она вплотную примкнет к основе. Так, для ограды протяженностью 50 метров потребуется 50 метров
строительной сетки.
С длиной все понятно, а что касается высоты, стоит запомнить: нельзя покупать рабицу высотой с саму опору. Она
должна быть меньше ее ровно на то количество метров, которое будет погружено под землю. Обычно это метр, поэтому
стандартными показателями считаются строительные материалы высотой 1,2 и 2,2 метра соответственно.
Если вы решили усложнить себе задачу и сделать отдельные секции между основаниями, то рассчитать забор из
сетки-рабицы будет гораздо сложнее. Потребуются замеры секций, умноженные на их количество. Только так можно
получить точный метраж требуемого материала.
Цена не рассчитывается точно при запуске Calc. Функция «Остаточное использование» в журнале заданий, в котором используется дополнительная единица измерения (UoM) в Microsoft Dynamics NAV 5.0 с пакетом обновления 1
Быстро публикуемые статьи предоставляют информацию непосредственно из службы поддержки Microsoft. Информация, содержащаяся в данном документе, создана в ответ на возникающие или уникальные темы или предназначена для дополнения другой информации Базы знаний.
Эта статья относится к Microsoft Dynamics NAV для всех стран и всех языковых стандартов.
Предположим, что у вас есть элемент с дополнительной единицей измерения (UoM) в Microsoft Dynamics NAV 5.0 с пакетом обновления 1. Эта дополнительная единица измерения используется в диалоговом окне Job Item Price . Когда вы запускаете Calc. Оставшаяся функция использования в журнале вакансий, цена не рассчитана точно. Вместо этого Microsoft Dynamics NAV использует значение Кол-во на единицу измерения для расчета цены за единицу. Следовательно, цена за единицу неверна.
Оставшаяся функция использования в журнале вакансий, цена не рассчитана точно. Вместо этого Microsoft Dynamics NAV использует значение Кол-во на единицу измерения для расчета цены за единицу. Следовательно, цена за единицу неверна.
Симптомы
Информация об исправлении
Поддерживаемое исправление теперь доступно от Microsoft.Однако он предназначен только для устранения проблемы, описанной в этой статье. Применяйте его только к системам, в которых возникает эта конкретная проблема. Это исправление может пройти дополнительное тестирование. Таким образом, если вы не сильно подвержены этой проблеме, мы рекомендуем дождаться следующего пакета обновления Microsoft Dynamics NAV 5.0 или следующей версии Microsoft Dynamics NAV, содержащей это исправление.
Примечание. В особых случаях расходы, которые обычно взимаются за обращение в службу поддержки, могут быть отменены, если специалист службы технической поддержки для Microsoft Dynamics и связанных продуктов определит, что конкретное обновление решит вашу проблему.Обычные расходы на поддержку будут применяться к дополнительным вопросам поддержки и проблемам, которые не соответствуют требованиям для конкретного рассматриваемого обновления.
Разрешение
Информация по установке
Microsoft предоставляет примеры программирования только для иллюстрации, без явных или подразумеваемых гарантий. Это включает, но не ограничивается, подразумеваемые гарантии товарной пригодности или пригодности для определенной цели.В этой статье предполагается, что вы знакомы с демонстрируемым языком программирования и инструментами, которые используются для создания и отладки процедур. Инженеры службы поддержки Майкрософт могут помочь объяснить функциональность конкретной процедуры, но они не будут изменять эти примеры для предоставления дополнительных функций или построения процедур в соответствии с вашими конкретными требованиями.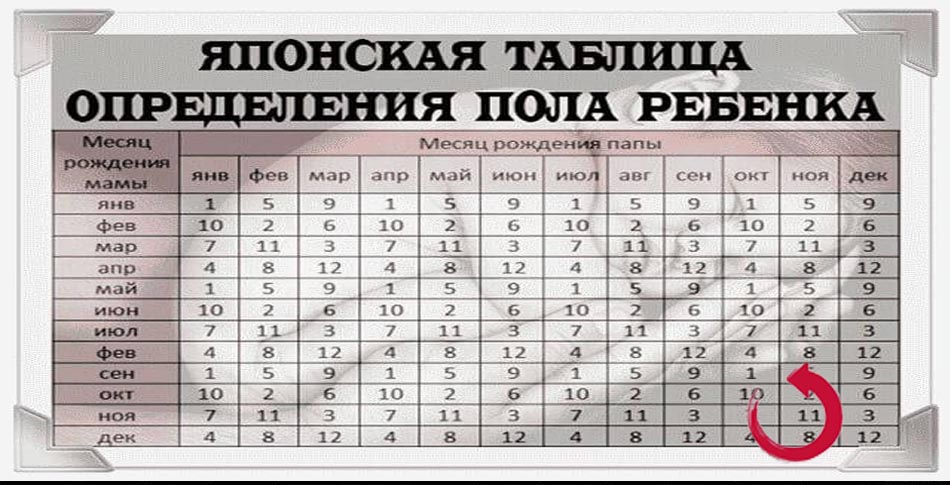
Примечание. Перед установкой этого исправления убедитесь, что все пользователи клиента Microsoft Navision вышли из системы.Сюда входят пользователи клиентов Microsoft Navision Application Services (NAS). Вы должны быть единственным клиентским пользователем, который вошел в систему при установке этого исправления.
Для установки этого исправления необходима лицензия разработчика.
Мы рекомендуем, чтобы учетной записи пользователя в окне входа в Windows или в окне входа в базу данных был назначен идентификатор роли «SUPER». Если учетной записи пользователя не может быть назначен идентификатор роли «SUPER», необходимо убедиться, что учетная запись пользователя имеет следующие разрешения:
Разрешение на изменение для объекта, который вы будете изменять.
Разрешение на выполнение для объекта с идентификатором системного объекта 5210 и для объекта с идентификатором системного объекта 9015.
Примечание. У вас нет прав на хранилища данных, если вам не нужно выполнять восстановление данных.
Изменения кода
Примечание. Всегда проверяйте исправления кода в контролируемой среде, прежде чем применять исправления к рабочим компьютерам.
Чтобы решить эту проблему, измените код в функции CopyJobItemPriceToJobJnlLine в калькуляторе Sales Price Calc. Mgt. codeunit (7000) следующим образом:
Существующий код
...
WITH JobJnlLine DO BEGIN
IF JobItemPrice. "Apply Job Price" THEN BEGIN// Удалите следующую строку.
«Цена за единицу»: = JobItemPrice. «Цена за единицу» * «Кол-во на единицу измерения»;
// Конец строки.«Фактор стоимости»: = JobItemPrice. «Коэффициент стоимости единицы»;
END;
IF JobItemPrice."Применить скидку на вакансию" THEN
"Line Discount%": = JobItemPrice. "Line Discount%";
конец;
...
Код замены
...
WITH JobJnlLine DO BEGIN
IF JobItemPrice. "Apply Job Price" THEN BEGIN// Добавьте следующую строку.
«Цена за единицу»: = JobItemPrice."Цена за единицу";
// Конец строки.«Фактор стоимости»: = JobItemPrice. «Коэффициент стоимости единицы»;
END;
IF JobItemPrice. "Применить скидку на вакансию" THEN
"Line Discount%": = JobItemPrice. "Line Discount%";
конец;
...
Предварительные требования
Для установки этого исправления необходимо иметь пакет обновления 1 для Microsoft Dynamics NAV 5.0.
Информация об удалении
Это исправление удалить нельзя.
Microsoft подтвердила, что это проблема продуктов Microsoft, перечисленных в разделе «Относится к».
Статус
MICROSOFT И / ИЛИ ЕГО ПОСТАВЩИКИ НЕ ДЕЛАЮТ НИКАКИХ ЗАЯВЛЕНИЙ ИЛИ ГАРАНТИЙ В ОТНОШЕНИИ СООТВЕТСТВИЯ, НАДЕЖНОСТИ ИЛИ ТОЧНОСТИ ИНФОРМАЦИИ, СОДЕРЖАЩЕЙСЯ В ДОКУМЕНТАЦИИ И СООТВЕТСТВУЮЩЕЙ ГРАФИКЕ, РАЗМЕЩЕННОЙ НА ЭТОМ ВЕБ-САЙТЕ.
МАТЕРИАЛЫ МОГУТ СОДЕРЖАТЬ ТЕХНИЧЕСКИЕ НЕТОЧНОСТИ ИЛИ ТИПОГРАФИЧЕСКИЕ ОШИБКИ И МОГУТ БЫТЬ ПЕРЕСМОТРЕНЫ В ЛЮБОЕ ВРЕМЯ БЕЗ УВЕДОМЛЕНИЯ. В МАКСИМАЛЬНОЙ СТЕПЕНИ, РАЗРЕШЕННОЙ ДЕЙСТВУЮЩИМ ЗАКОНОДАТЕЛЬСТВОМ, МАЙКРОСОФТ И / ИЛИ ЕГО ПОСТАВЩИКИ ОТКАЗЫВАЮТСЯ И ИСКЛЮЧАЮТ ВСЕ ЗАЯВЛЕНИЯ, ГАРАНТИИ И УСЛОВИЯ, ЯВНЫЕ, ПОДРАЗУМЕВАЕМЫЕ ИЛИ ЗАКОНОДАТЕЛЬНЫЕ УСЛОВИЯ, ВКЛЮЧАЯ, НО НЕ ОГРАНИЧИВАЕМЫЕ, ОБЯЗАТЕЛЬСТВА ИЛИ ГАРАНТИИ. УДОВЛЕТВОРИТЕЛЬНОЕ СОСТОЯНИЕ ИЛИ КАЧЕСТВО, КОММЕРЧЕСКАЯ ЦЕННОСТЬ И ПРИГОДНОСТЬ ДЛЯ ОПРЕДЕЛЕННОЙ ЦЕЛИ В ОТНОШЕНИИ МАТЕРИАЛОВ.
Точность, прецизионность и значащие цифры
Цели обучения
К концу этого раздела вы сможете:
- Определите необходимое количество значащих цифр как при сложении, так и при вычитании, а также при вычислениях умножения и деления.
- Рассчитайте процент погрешности измерения.
Точность и прецизионность измерения
Наука основана на наблюдении и эксперименте, то есть на измерениях. Точность — это насколько измерение близко к правильному значению для этого измерения. Например, предположим, что вы измеряете длину стандартной компьютерной бумаги. На упаковке, в которой вы приобрели бумагу, указано, что ее длина составляет 11 дюймов. Вы трижды измеряете длину бумаги и получаете следующие размеры: 11,1 дюйма, 11,2 дюйма и 10,9 дюйма. Эти измерения довольно точны, поскольку они очень близки к правильному значению в 11,0 дюймов. Напротив, если бы вы получили размер в 12 дюймов, ваше измерение не было бы очень точным.
Точность измерительной системы означает, насколько близко согласие между повторными измерениями (которые повторяются в одних и тех же условиях). Рассмотрим пример бумажных мерок. Точность измерений относится к разбросу измеренных значений. Один из способов анализа точности измерений — определение диапазона или разницы между самым низким и самым высоким измеренными значениями. В этом случае наименьшее значение было 10.9 дюймов, а максимальное значение составляло 11,2 дюйма. Таким образом, измеренные значения отклонялись друг от друга не более чем на 0,3 дюйма. Эти измерения были относительно точными, поскольку они не слишком сильно различались по величине. Однако, если бы измеренные значения были 10,9, 11,1 и 11,9, тогда измерения не были бы очень точными, потому что были бы значительные отклонения от одного измерения к другому.
Измерения в бумажном примере точны и точны, но в некоторых случаях измерения точны, но не точны, или они точны, но неточны. Давайте рассмотрим пример системы GPS, которая пытается определить местоположение ресторана в городе. Представьте, что ресторан находится в центре мишени в яблочко, и думайте о каждой попытке GPS определить местонахождение ресторана как о черной точке. На рисунке 3 вы можете видеть, что измерения GPS разнесены далеко друг от друга, но все они относительно близки к фактическому местоположению ресторана в центре цели. Это указывает на низкую точность измерительной системы с высокой точностью.Однако на рисунке 4 измерения GPS сосредоточены довольно близко друг к другу, но они находятся далеко от целевого местоположения. Это указывает на высокую точность измерительной системы с низкой точностью.
Давайте рассмотрим пример системы GPS, которая пытается определить местоположение ресторана в городе. Представьте, что ресторан находится в центре мишени в яблочко, и думайте о каждой попытке GPS определить местонахождение ресторана как о черной точке. На рисунке 3 вы можете видеть, что измерения GPS разнесены далеко друг от друга, но все они относительно близки к фактическому местоположению ресторана в центре цели. Это указывает на низкую точность измерительной системы с высокой точностью.Однако на рисунке 4 измерения GPS сосредоточены довольно близко друг к другу, но они находятся далеко от целевого местоположения. Это указывает на высокую точность измерительной системы с низкой точностью.
Точность, прецизионность и неопределенность
Степень точности и прецизионности измерительной системы связана с погрешностью измерений. Неопределенность — это количественная мера того, насколько ваши измеренные значения отклоняются от стандартного или ожидаемого значения.Если ваши измерения не очень точны или точны, то неопределенность ваших значений будет очень высокой. В более общем плане неопределенность можно рассматривать как отказ от ответственности за ваши измеренные значения. Например, если кто-то попросил вас указать пробег вашего автомобиля, вы можете сказать, что это 45 000 миль, плюс-минус 500 миль. Сумма плюс или минус — это неопределенность в вашей стоимости. То есть вы указываете, что фактический пробег вашего автомобиля может составлять от 44 500 миль до 45 500 миль или где-то посередине.Все измерения содержат некоторую неопределенность. В нашем примере измерения длины бумаги мы могли бы сказать, что длина бумаги составляет 11 дюймов, плюс-минус 0,2 дюйма. Неопределенность измерения, A , часто обозначается как δ A ( «Дельта A»), поэтому результат измерения будет записан как A ± δ A . В нашем примере с бумагой длина бумаги может быть выражена как 11 дюймов ± 0,2.
Факторы, способствующие неопределенности измерения, включают:
- Ограничения измерительного прибора,
- Навык человека, производящего измерение,
- Неровности в измеряемом объекте,
- Любые другие факторы, влияющие на результат (сильно зависят от ситуации).

В нашем примере такими факторами, способствующими неопределенности, могут быть следующие: наименьшее деление на линейке — 0,1 дюйма, у человека, использующего линейку, плохое зрение, или одна сторона листа бумаги немного длиннее другой. В любом случае неопределенность измерения должна основываться на тщательном рассмотрении всех факторов, которые могут внести свой вклад, и их возможных последствий.
Установление связей: связи в реальном мире — лихорадка или озноб?
Неопределенность — важная часть информации как в физике, так и во многих других реальных приложениях.Представьте, что вы ухаживаете за больным ребенком. Вы подозреваете, что у ребенка жар, поэтому проверяете его температуру с помощью термометра. Что, если бы погрешность термометра была 3º? Если температура ребенка была 37ºC (что является нормальной температурой тела), «истинная» температура могла бы быть где угодно от гипотермических 34º до опасно высоких 40º. Термометр с погрешностью 3º бесполезен.
Один из методов выражения неопределенности — это процент от измеренного значения.Если результат измерения A выражается с неопределенностью, δ A , процент неопределенности (% unc) определяется как
[латекс] \% \ text {unc} = \ frac {\ delta {A}} {A} \ times100 \% [/ latex]
Пример 1: Расчет процента неопределенности: мешок яблок
В продуктовом магазине продаются 5-фунтовые мешки яблок. Вы покупаете четыре пакета в течение месяца и каждый раз взвешиваете яблоки. Вы получите следующие размеры:
- Неделя 1 вес: 4.8 фунтов
- Неделя 2 Вес: 5,3 фунта
- Неделя 3 Вес: 4,9 фунта
- Неделя 4 Вес: 5,4 фунта
Вы определили, что вес 5-фунтового мешка имеет погрешность ± 0,4 фунта. Какова погрешность веса мешка в процентах?
Стратегия
Во-первых, обратите внимание, что ожидаемое значение веса мешка, A , составляет 5 фунтов. Неопределенность этого значения, δ A , составляет 0,4 фунта. Мы можем использовать следующее уравнение для определения процентной погрешности веса. :
Неопределенность этого значения, δ A , составляет 0,4 фунта. Мы можем использовать следующее уравнение для определения процентной погрешности веса. :
[латекс] \% \ text {unc} = \ frac {\ delta {A}} {A} \ times100 \% [/ latex]
Решение
Подставьте известные значения в уравнение:
[латекс] \% \ text {unc} = \ frac {0.4 \ text {lb}} {5 \ text {lb}} \ times100 \% = 8 \% [/ latex]
Обсуждение
Можно сделать вывод, что вес мешка с яблоками составляет 5 фунтов ± 8%. Подумайте, как изменился бы этот процент неопределенности, если бы мешок с яблоками был вдвое тяжелее, но неопределенность в весе осталась бы прежней. Совет для будущих расчетов: при вычислении процентной погрешности всегда помните, что вы должны умножить дробь на 100%. Если вы этого не сделаете, у вас будет десятичное количество, а не процентное значение.
Неопределенности в расчетах
Есть неопределенность во всех вычислениях на основе измеренных величин. Например, площадь пола, рассчитанная на основе измерений его длины и ширины, имеет неопределенность, поскольку длина и ширина имеют неопределенности. Насколько велика неопределенность в том, что вы вычисляете умножением или делением? Если измерения, входящие в расчет, имеют небольшую погрешность (несколько процентов или меньше), то метод сложения процентов можно использовать для умножения или деления.Этот метод говорит, что процент погрешности в величине, вычисленной путем умножения или деления, представляет собой сумму процентных погрешностей в элементах, использованных для выполнения расчета . Например, если пол имеет длину 4,00 м и ширину 3,00 м с погрешностями 2% и 1% соответственно, то площадь пола составляет 12,0 м 2 и имеет погрешность 3. (Выраженная как площадь, это 0,36 м 2 , которую мы округляем до 0,4 м 2 , так как площадь этажа отводится на десятые доли квадратного метра. )
)
Проверьте свое понимание
Тренер средней школы по легкой атлетике только что купил новый секундомер. В руководстве по секундомеру указано, что погрешность секундомера составляет ± 0,05 с. Бегуны из команды тренера по легкой атлетике регулярно измеряют 100-метровые спринты за время от 11,49 до 15,01 с. На последних соревнованиях по бегу в школе спринтер, занявший первое место, показал результат за 12,04 секунды, а спринтер, занявший второе место, — за 12,07 секунды. Поможет ли новый секундомер тренера рассчитать время спринтерской команды? Почему или почему нет?
Решение
Нет, погрешность секундомера слишком велика, чтобы эффективно различать время спринта.
Прецизионность измерительных инструментов и значимых фигур
Важным фактором точности измерений является точность измерительного инструмента. В общем, точный измерительный инструмент — это инструмент, который может измерять значения с очень маленькими приращениями. Например, стандартная линейка может измерять длину с точностью до миллиметра, а штангенциркуль — с точностью до 0,01 миллиметра. Штангенциркуль — более точный измерительный инструмент, поскольку он может измерять очень небольшие различия в длине.Чем точнее измерительный инструмент, тем точнее и точнее могут быть измерения.
Когда мы выражаем измеренные значения, мы можем перечислить только столько цифр, сколько мы первоначально измерили с помощью нашего измерительного инструмента. Например, если вы используете стандартную линейку для измерения длины палки, вы можете измерить ее и получить 36,7 см. Вы не можете выразить это значение как 36,71 см, потому что ваш измерительный инструмент не был достаточно точным, чтобы измерить сотую долю сантиметра. Следует отметить, что последняя цифра в измеренном значении была определена каким-то образом лицом, выполняющим измерение.Например, человек, измеряющий длину палки линейкой, замечает, что длина палки находится где-то между 36,6 и 36,7 см, и он или она должны оценить значение последней цифры. При использовании метода значащих цифр правило состоит в том, что последняя цифра, записанная в измерении, является первой цифрой с некоторой неопределенностью . Чтобы определить количество значащих цифр в значении, начните с первого измеренного значения слева и подсчитайте количество цифр до последней цифры, записанной справа.Например, измеренное значение 36,7 см состоит из трех цифр или значащих цифр. Значительные цифры указывают на точность измерительного инструмента, который использовался для измерения значения.
При использовании метода значащих цифр правило состоит в том, что последняя цифра, записанная в измерении, является первой цифрой с некоторой неопределенностью . Чтобы определить количество значащих цифр в значении, начните с первого измеренного значения слева и подсчитайте количество цифр до последней цифры, записанной справа.Например, измеренное значение 36,7 см состоит из трех цифр или значащих цифр. Значительные цифры указывают на точность измерительного инструмента, который использовался для измерения значения.
Нули
Особое внимание уделяется нулям при подсчете значащих цифр. Нули в 0,053 не имеют значения, потому что они только хранители места, которые определяют местонахождение десятичной точки. В 0,053 есть две значащих цифры. Нули в 10.053 не являются заместителями, но значимы — это число состоит из пяти значащих цифр.Нули в 1300 могут иметь или не иметь значения в зависимости от стиля написания чисел. Они могли означать, что число известно с точностью до последней цифры, или они могли быть помощниками. Итак, 1300 может иметь две, три или четыре значащих цифры. (Чтобы избежать этой двусмысленности, напишите 1300 в экспоненциальной системе счисления.) Нули имеют значение, кроме случаев, когда они служат только в качестве заместителей .
Проверьте свое понимание
Определите количество значащих цифр в следующих измерениях:
- 0.0009
- 15 450,0
- 6 × 10 3
- 87,990
- 30,42
Решения
(а) 1; нули в этом номере — это метки, обозначающие десятичную запятую
(б) 6; здесь нули указывают на то, что измерение было выполнено с точностью до десятичной запятой 0,1, поэтому нули значимы
(с) 1; значение 10 3 означает десятичный разряд, а не количество измеренных значений
(д) 5; последний ноль указывает на то, что измерение было выполнено до 0. 001 десятичная точка, значит значащая
001 десятичная точка, значит значащая
(е) 4; любые нули, расположенные между значащими цифрами в числе, также имеют значение
Значимые цифры в расчетах
При объединении измерений с разной степенью точности и точности, количество значащих цифр в окончательном ответе не может быть больше количества значащих цифр в наименее точном измеренном значении . Есть два разных правила, одно для умножения и деления, а другое для сложения и вычитания, как обсуждается ниже.
1. Для умножения и деления: Результат должен иметь такое же количество значащих цифр, что и количество, имеющее младшие значащие цифры, участвующие в вычислении . Например, площадь круга можно вычислить по его радиусу, используя A = πr 2 . Посмотрим, сколько значащих цифр имеет площадь, если в радиусе всего два, скажем, r = 1,2 м. Затем
A = π r 2 = (3.1415927…) × (1,2 м) 2 = 4,5238934 м 2
— это то, что вы получили бы, используя калькулятор с восьмизначным выводом. Но поскольку радиус состоит только из двух значащих цифр, он ограничивает вычисляемую величину двумя значащими цифрами или A = 4,5 м 2 , даже если π является хорошим числом по крайней мере до восьми цифр.
2. Для сложения и вычитания: Ответ не может содержать больше десятичных знаков, чем наименее точное измерение . Предположим, вы купили в продуктовом магазине 7,56 кг картофеля, измеренного на шкале с точностью 0,01 кг. Затем вы бросаете в свою лабораторию 6,052 кг картофеля, измеренного по шкале с точностью 0,001 кг. Наконец, вы идете домой и добавляете 13,7 кг картофеля, как измерено весами для ванной с точностью 0,1 кг. Сколько у вас сейчас килограммов картошки и сколько значащих цифр уместно в ответе? Масса находится простым сложением и вычитанием:
7.56 кг — 6,052 кг + 13,7 кг = 15,208 кг = 15,2 кг
Далее мы определяем наименее точное измерение: 13,7 кг. Это измерение выражается с точностью до 0,1 десятичного знака, поэтому наш окончательный ответ также должен быть выражен с точностью до 0,1. Таким образом, ответ округляется до десятого места, что дает нам 15,2 кг.
Значимые цифры в этом тексте
В этом тексте предполагается, что большинство чисел состоит из трех значащих цифр. Кроме того, во всех проработанных примерах используется постоянное количество значащих цифр.Вы заметите, что ответ, данный для трех цифр, основан, например, на правильности ввода как минимум трех цифр. Если на входе меньше значащих цифр, в ответе также будет меньше значащих цифр. Также уделяется внимание тому, чтобы количество значащих цифр соответствовало создаваемой ситуации. В некоторых темах, особенно в оптике, необходимы более точные числа и будут использоваться более трех значащих цифр. Наконец, если число точное , такое как два в формуле для длины окружности, c = 2π r , это не влияет на количество значащих цифр в вычислении.
Проверьте свое понимание
Выполните следующие вычисления и выразите свой ответ, используя правильное количество значащих цифр.
(a) У женщины есть две сумки весом 13,5 фунтов и одна сумка весом 10,2 фунтов. Какой общий вес пакетов?
(b) Сила F , действующая на объект, равна его массе m, умноженной на его ускорение a. Если вагон массой 55 кг ускоряется со скоростью 0,0255 м / с 2 , какова сила, действующая на вагон? (Единица силы называется ньютоном и обозначается символом N.)
Решения
(a) 37,2 фунта; Поскольку количество сумок является точным значением, оно не учитывается в значащих цифрах.
(б) 1,4 Н; Поскольку значение 55 кг состоит только из двух значащих цифр, окончательное значение также должно содержать две значащие цифры.
Исследования PhET: оценка
Оцените размер в одном, двух и трех измерениях! Несколько уровней сложности позволяют постепенно улучшать навыки.
Сводка
- Точность измеренного значения означает, насколько близко результат измерения к правильному значению. Неопределенность измерения — это оценка того, на какую величину результат измерения может отличаться от этого значения.
- Точность измеренных значений означает, насколько близко согласие между повторными измерениями.
- Точность измерительного инструмента связана с размером его шага измерения.Чем меньше шаг измерения, тем точнее инструмент.
- Значительные цифры показывают точность измерительного инструмента.
- При умножении или делении измеренных значений окончательный ответ может содержать столько значащих цифр, сколько наименее точное значение.
- При сложении или вычитании измеренных значений окончательный ответ не может содержать больше десятичных знаков, чем наименее точное значение.
Концептуальные вопросы
1. Какова связь между точностью и неопределенностью измерения?
2.Рецепты для коррекции зрения даются в единицах, которые называются диоптриями (D). Определите значение этой единицы. Получите информацию (возможно, позвонив окулисту или выполнив поиск в Интернете) о минимальной неопределенности, с которой определяются поправки в диоптриях, и о точности, с которой могут быть произведены корректирующие линзы. Обсудите источники неопределенностей как в рецепте, так и в точности изготовления линз.
Избранные решения проблем и упражнения
1.2 кг
3. (a) от 85,5 до 94,5 км / ч (b) от 53,1 до 58,7 миль / ч
5. (а) 7,6 × 10 7 ударов (б) 7,57 × 10 7 ударов (в) 7,57 × 10 7 ударов
7. (а) 3 (б) 3 (в) 3
9. (а) 2,2% (б) от 59 до 61 км / ч
11. 80 ± 3 уд / мин
13. 2,6 ч
15. 11 ± 1 см 3
17. 12.06 ± 0,04 м 2
Калькулятор точности
Наш калькулятор точности — это простой инструмент, который позволяет вычислять точность тремя различными методами .В то время как первые два метода широко используются в оценке диагностических тестов , третий метод может быть применен к широкому кругу наук ⚗️
Несколько минут, потраченных на статью ниже, научат вас использованию точности в статистике , фундаментальным различиям между точностью и точностью , а также всем формулам, используемым в расчетах точности .
Как пользоваться калькулятором точности?
Точность вычислений требует различных решений для разных задач .Внимательно прочтите приведенную ниже инструкцию и решите, какой метод лучше всего подходит для вашей ситуации :
Взгляните на свои данные :
Вы рассчитываете точность диагностического теста?
Если соотношение пациентов с заболеванием и пациентов без заболевания отражает распространенность заболевания, используют стандартный метод № 1 .
Если соотношение пациентов с заболеванием и пациентов без заболевания не отражает распространенности заболевания, используют метод распространенности № 2 .
Вы пытаетесь найти точность, используя простую процентную ошибку?
- Используйте метод процентной ошибки № 3 .
| 💡 Наш калькулятор автоматически рассчитает чувствительность и специфичность теста, необходимого для метода № 2 , как только вы введете все значения истинно отрицательного / положительного и ложно отрицательного / положительного для метода № 1. |
Вы уже нашли то, что вам нужно? Попробуйте другие наши полезные инструменты статистики:
Как рассчитать процент точности?
Следуйте нашему простому руководству, чтобы узнать, как измерить точность во всех возможных ситуациях:
Стандартное уравнение точности для диагностического теста, используемое в методе № 1
Используется, если соотношение пациентов с заболеванием (истинно положительный, ложноотрицательный) и пациентов без заболевания (истинно отрицательный, ложноположительный) отражает распространенность заболевания .
Точность = (TP + TN) / (TP + TN + FP + FN)Где:
- ТП — истинно положительный;
- TN — истинно отрицательный;
- FP — ложное срабатывание; и
- FN — ложноотрицательный.
Формула для расчета точности на основе распространенности — метод № 2
Точность = ((Чувствительность) * (Распространенность)) + ((Специфичность) * (1 - Распространенность))Где:
-
Чувствительность = TP / (TP + FN), дана в%; -
Специфичность = TN / (FP + TN), дано в%; и - Распространенность — количество населения, которое болеет заболеванием в определенное время, выраженное в%.
-
Погрешность в процентах / формула точности в процентах — метод № 3
Ошибка в процентах = (| (V o - Vₐ) | / Vₐ) * 100Где:
- V o — наблюдаемое значение;
- V a — значение принято за истину; и
- | (V o — Vₐ) | — абсолютное неотрицательное значение.
Это сообщает нам о точности чтения — насколько наблюдаемое значение основано на истине.
Чем больше ошибка, тем ниже точность.
Пример расчета точности:
Мы испытываем наш новый термометр. Наша измеренная температура равна 95 ° F. Мы знаем, что наша средняя температура равна 97,8 ° F.
Воспользуемся методом № 3:
- Наблюдаемое значение: 95
- Принятое значение: 98,7
Ошибка в процентах = (| 95 - 97,8 | / 97,8) * 100 = (2,8 / 97,8) * 100 = 0,0286 * 100 = 2,86%
Точность vs.точность
Точность измеряет, насколько близко данное значение к истине (или значению, согласованному и подтвержденному многими учеными).
Точность измеряет, насколько данные измерения близки друг к другу . Другими словами, он описывает, насколько часто повторяется данный результат — его воспроизводимость.
Что такое точность в химии?
Точность по химии требует калибровки . Сначала необходимо сравнить аналитический метод с известным стандартом.
Стандарт данного вещества должен быть чистым , не содержать молекул воды и быть стабильным.
Калибровка — это процесс сравнения результатов, полученных с помощью нашего устройства, с устройством известного и подтвержденного качества. Титрование может быть хорошим примером процесса калибровки.
Как рассчитать точность измерений
Обновлено 2 ноября 2020 г.
Кевин Бек
Наука в значительной степени основана на поддающихся количественной оценке данных.Сбор полезных данных, в свою очередь, зависит от каких-то измерений, причем масса, площадь, объем, скорость и время являются одними из этих критически важных показателей.
Очевидно, что точность, которая описывает, насколько близко измеренное значение приближается к его истинному значению, жизненно важна во всех научных начинаниях. Это верно не только по наиболее очевидным, актуальным причинам, таким как необходимость знать температуру на улице, чтобы правильно одеться, но и потому, что неточные измерения сегодня приводят к накоплению неверных данных в долгосрочной перспективе.Если данные о погоде, которые вы собираете прямо сейчас, неверны, климатические данные, которые вы просматриваете в отношении 2018 года в будущем, также будут неправильными.
Чтобы определить точность измерения, обычно необходимо знать истинное значение в природе этого измерения. Например, «справедливая» монета, подброшенная очень много раз, должна выпадать орлом в 50% случаев и решкой в 50% случаев, согласно теории вероятностей. В качестве альтернативы, чем более воспроизводимо измерение (то есть, чем выше его точность ), тем более вероятно, что значение будет близко к реальному значению в природе.Если оценки чьего-либо роста, основанные на показаниях 50 очевидцев, находятся в диапазоне от 5 футов 8 дюймов до 6 футов 0 дюймов, вы можете с большей уверенностью заключить, что рост человека близок к 5 футов 10 дюймов, чем если бы оценки варьировались. между 5’2 «и 6’6», несмотря на то, что последнее дает такое же среднее значение 5’10 дюймов.
Для определения точности измерений экспериментальным путем необходимо определить их , отклонение .
Соберите как можно больше измерений того, что вы измеряете
Позвоните по этому номеру N .Если вы оцениваете температуру с помощью разных термометров неизвестной точности, используйте как можно больше разных термометров.
Найдите среднее значение ваших измерений
Сложите измерения и разделите на N . Если у вас есть пять термометров и измерения по Фаренгейту составляют 60 °, 66 °, 61 °, 68 ° и 65 °, среднее значение будет
\ frac {60 + 66 + 61 + 68 + 65} {5} = \ frac {320} {5} = 64 °
Найдите абсолютное значение отличия каждого отдельного измерения от среднего
Это дает отклонение каждого измерения.Причина, по которой необходимо абсолютное значение, заключается в том, что некоторые измерения будут меньше истинного значения, а некоторые — больше; простое сложение сырых значений приведет к нулю и ничего не скажет о процессе измерения.
Найдите среднее значение всех отклонений, сложив их и разделив на N
Полученная статистика предлагает косвенную оценку точности ваших измерений. Чем меньшую долю самого измерения представляет собой отклонение, тем больше вероятность того, что ваше измерение будет точным, хотя необходимо знать истинное значение, чтобы быть в этом абсолютно уверенным.Таким образом, если возможно, сравните результат с эталонным значением, например, в данном случае с официальными данными о температуре от Национальной службы погоды.
Расчет абсолютной точности или точности системы
Затем вычислите Абсолютная точность для каждого компонента.
Для любого отдельного устройства с усилением (усилителя или аттенюатора) для указанного номинального диапазона National Instruments предоставляет характеристики абсолютной точности в милливольтах. В зависимости от представления различных ошибок для расчета точности используются три различных уравнения.Все уравнения перечислены ниже:
Уравнение 1:
Абсолютная точность = ± [( VoltageReading x GainError ) + ( VoltageRange x OffsetError ) + NoiseUncertainty ]
Где:
Вы можете получить значения параметров в приведенном выше уравнении, просмотрев спецификации, содержащиеся в руководстве, спецификациях или технических характеристиках каждого компонента.
Уравнение 2:
Абсолютная точность = ± [( Входное напряжение x% показания ) + ( Диапазон напряжения x Смещение ) + Системный шум + Температурный дрейф ]
Где:
Значения параметров в приведенном выше уравнении можно получить, просмотрев информацию, содержащуюся в спецификациях каждого компонента, руководстве или таблице.
Уравнение 3:
Модули серии
C предоставляют краткие спецификации для пользователей, чтобы определить их точность во всем диапазоне рабочих температур (откалиброванный максимум от -40 до 70). Этот ввод точности учитывает колебания температуры, наихудшие допуски компонентов, тепловой гистерезис и т. Д.
Абсолютная точность = ± [( InputReading x GainError ) + (Range x OffsetError) + InputNoise ]
Где:
- Входное чтение — это значение, которое пользователь пытается измерить
- Gain Error — грубая погрешность в%, основанная на входном усилении
- Диапазон — диапазон считывания, на который настроено устройство.Например, от 0 до 10 В, диапазон = 10
- OffsetError — максимальная ошибка смещения. В таблице это может быть указано в ppm вместо%, для преобразования в процент используйте 1% = 10 000ppm.
- InputNoise — это ошибка, вносимая в измерения самим устройством. См. Примечания в разделе дополнительной информации. На изображении ниже показан пример того, какие значения использовать.
.
Все вышеперечисленные характеристики можно найти в таблице данных или технических характеристиках компонента.
1.5 Погрешность, точность и прецизионность измерений — химия
Цели обучения
К концу этого раздела вы сможете:
- Определите точность и прецизионность
- Различают точные и неопределенные числа
- Правильно представить неопределенность величин с помощью значащих цифр
- Применить правильные правила округления к вычисленным количествам
Подсчет — это единственный тип измерения, в котором отсутствует неопределенность, при условии, что количество подсчитываемых объектов не изменяется во время процесса подсчета.Результатом такого счетного измерения является пример точного числа . Если мы посчитаем яйца в коробке, мы точно знаем, что — это , сколько яиц в коробке. Количество определенных количеств также является точным. По определению, 1 фут составляет ровно 12 дюймов, 1 дюйм — ровно 2,54 сантиметра, а 1 грамм — ровно 0,001 килограмма. Однако величины, полученные на основе измерений, отличных от счета, являются неопределенными в различной степени из-за практических ограничений используемого процесса измерения.
Количество измеренных величин, в отличие от определенных или непосредственно подсчитываемых величин, неточно. Чтобы измерить объем жидкости в градуированном цилиндре, вы должны снять показания на дне мениска, самой нижней точке на изогнутой поверхности жидкости.
Рис. 1. Чтобы измерить объем жидкости в этом градуированном цилиндре, вы должны мысленно разделить расстояние между отметками 21 и 22 мл на десятые доли миллилитра, а затем произвести измерение (оценку) внизу мениска.
См. Рисунок на рисунке 1. Нижняя часть мениска в этом случае явно находится между отметками 21 и 22, что означает, что объем жидкости составляет , безусловно, больше 21 мл, но меньше 22 мл. Мениск кажется немного ближе к отметке 22 мл, чем к отметке 21 мл, поэтому разумная оценка объема жидкости будет 21,6 мл. Таким образом, в числе 21.6 цифры 2 и 1 являются точными, но цифра 6 является приблизительной. Некоторые люди могут оценить положение мениска как одинаково удаленное от каждой отметки и оценить цифру десятого места как 5, в то время как другие могут подумать, что она еще ближе к отметке 22 мл, и оценить эту цифру как 7.Обратите внимание, что было бы бессмысленно пытаться оценить цифру для сотых разрядов, учитывая, что цифра десятых разряда неопределенна. Как правило, числовые шкалы, такие как шкала на этом градуированном цилиндре, позволяют выполнять измерения с точностью до одной десятой наименьшего деления шкалы. В этом случае шкала имеет деление по 1 мл, поэтому объемы могут быть измерены с точностью до 0,1 мл.
Эта концепция верна для всех измерений, даже если вы не делаете оценку активно. Если вы поместите четверть на стандартные электронные весы, вы можете получить показание 6.72 г. Цифры 6 и 7 являются точными, а цифра 2 указывает на то, что масса четверти, вероятно, составляет от 6,71 до 6,73 грамма. Четверть весит около 6,72 грамма, с номинальной погрешностью измерения ± 0,01 грамма. Если взвесить четверть на более чувствительных весах, мы можем обнаружить, что ее масса составляет 6,723 г. Это означает, что его масса составляет от 6,722 до 6,724 грамма, погрешность составляет 0,001 грамма. Каждое измерение имеет погрешность , которая зависит от используемого устройства (и возможностей пользователя).Все цифры в измерении, включая неопределенную последнюю цифру, называются значащими цифрами или значащими цифрами . Обратите внимание, что ноль может быть измеренным значением; например, если вы стоите на весах, которые показывают вес с точностью до фунта и показывают «120», то 1 (сотни), 2 (десятки) и 0 (единицы) являются значимыми (измеренными) значениями.
При правильном выполнении измерения все цифры в результате имеют значение. Но что, если бы вы анализировали заявленное значение и пытались определить, что важно, а что нет? Во-первых, все ненулевые цифры значимы, и только нули требуют некоторого размышления.Мы будем использовать термины «ведущий», «конечный» и «подчиненный» для нулей и рассмотрим, как с ними бороться.
Начиная с первой ненулевой цифры слева, отсчитайте эту цифру и все оставшиеся цифры справа. Это количество значащих цифр в измерении, если последняя цифра не является конечным нулем, лежащим слева от десятичной точки.
Невыполненные нули являются результатом измерения и поэтому всегда важны.Однако ведущие нули никогда не имеют значения — они просто говорят нам, где находится десятичная точка.
Начальные нули в этом примере не имеют значения. Мы могли бы использовать экспоненциальную запись (как описано в Приложении B) и выразить число как 8,32407 × 10 −3 ; тогда число 8.32407 содержит все значащие цифры, а 10 −3 определяет местонахождение десятичной точки.
Количество значащих цифр не определено в числе, оканчивающемся нулем слева от десятичной точки.Нули в измерении 1300 граммов могут иметь значение или они могут просто указывать, где находится десятичная точка. Неопределенность может быть разрешена с помощью экспоненциальной записи: 1,3 × 10 3 (две значащие цифры), 1,30 × 10 3 (три значащих цифры, если измерялись разряды десятков) или 1,300 × 10 3 (четыре значащих цифры, если также отмерялась единица). В случаях, когда доступно только число в десятичном формате, разумно предположить, что все нули в конце не имеют значения.
При определении значащих цифр обязательно обращайте внимание на сообщаемые значения и думайте об измерении и значащих цифрах с точки зрения того, что является разумным или вероятным при оценке того, имеет ли значение смысл. Например, официальная перепись населения в январе 2014 г. показала, что постоянное население США составляет 317 297 725 человек. Как вы думаете, правильно ли было определено население США по заявленным девяти значащим цифрам, то есть по точному количеству людей? Люди постоянно рождаются, умирают, переезжают в страну или из нее, и делаются предположения, чтобы учесть большое количество людей, которые фактически не учитываются.Из-за этих неопределенностей было бы более разумно ожидать, что мы знаем численность населения с точностью до миллиона или около того, и в этом случае численность населения должна быть представлена как 3,17 × 10 8 человек.
Второй важный принцип неопределенности заключается в том, что результаты, рассчитанные на основе измерения, по крайней мере так же неопределенны, как и само измерение. Мы должны принимать во внимание погрешность наших измерений, чтобы не искажать погрешность расчетных результатов.Один из способов сделать это — сообщить результат вычисления с правильным количеством значащих цифр, которое определяется следующими тремя правилами для округления чисел:
- Когда мы складываем или вычитаем числа, мы должны округлить результат до того же числа десятичных знаков, что и число с наименьшим числом десятичных знаков (наименее точное значение с точки зрения сложения и вычитания).
- Когда мы умножаем или делим числа, мы должны округлить результат до того же количества цифр, что и число с наименьшим числом значащих цифр (наименее точное значение с точки зрения умножения и деления).
- Если отбрасываемая цифра (цифра справа от сохраняемой цифры) меньше 5, мы «округляем вниз» и оставляем оставшуюся цифру без изменений; если больше 5, «округляем» и увеличиваем оставшуюся цифру на 1; если выпавшая цифра равна 5, мы округляем в большую или меньшую сторону, в зависимости от того, что дает четное значение для оставшейся цифры. (Последняя часть этого правила может показаться вам немного странной, но она основана на надежной статистике и направлена на то, чтобы избежать какого-либо смещения при отбрасывании цифры «5», поскольку она одинаково близка к обоим возможным значениям оставшейся цифры.)
Следующие примеры иллюстрируют применение этого правила при округлении нескольких различных чисел до трех значащих цифр:
- 0,028675 округляется до 0,0287 (пропущенная цифра 7 больше 5)
- 18,3384 округляет до 18,3 (выпавшая цифра 3 меньше 5)
- 6,8752 округляет «вверх» до 6,88 (пропущенная цифра 5, а оставшаяся цифра четная)
- 92,85 округляется до 92,8 (пропущенная цифра 5, а оставшаяся цифра четная)
Давайте рассмотрим эти правила на нескольких примерах.
Пример 1
Числа округления
Округлите следующее до указанного числа значащих цифр:
(а) 31,57 (с двумя значащими цифрами)
(б) 8,1649 (с тремя значащими цифрами)
(c) 0,051065 (до четырех значащих цифр)
(d) 0,
Решение
(a) 31,57 округляет «до» 32 (пропущенная цифра 5, а оставшаяся цифра четная)
(б) 8.1649 округляет до 8,16 (пропущенная цифра 4 меньше 5)
(c) 0,051065 округляется до 0,05106 (пропущенная цифра 5, а оставшаяся цифра четная)
(d) 0,
Проверьте свои знания
Округлите следующее до указанного числа значащих цифр:
(а) 0,424 (с двумя значащими цифрами)
(б) 0,0038661 (до трех значащих цифр)
(с) 421.25 (с четырьмя значащими цифрами)
(г) 28 683,5 (до пяти значащих цифр)
Ответ:
(а) 0,42; (б) 0,00387; (c) 421,2; (г) 28 684
Пример 2
Сложение и вычитание со значащими числами
Правило: когда мы складываем или вычитаем числа, мы должны округлять результат до того же количества десятичных знаков, что и число с наименьшим числом десятичных знаков (т. Е. Наименее точное значение в терминах). сложения и вычитания).
(a) Добавьте 1,0023 г и 4,383 г.
(b) Вычтем 421,23 г из 486 г.
Решение
(а) [латекс] \ displaystyle \ begin {array} {r} 1.0023 \ text {g} \\ +4.383 \; \; \ text {g} \\ \ hline 5.3853 \ text {g} \ end {array } [/ латекс]
Ответ 5,385 г (округление до тысячных; три десятичных знака)
(b) [латекс] \ displaystyle \ begin {array} {r} 486 \; \; \; \; \; \ text {g} \\ -421.23 \ text {g} \\ \ hline 64.77 \ text {g} \ end {array} [/ latex]
Ответ 65 г (округление до единицы; без десятичных знаков)
Проверьте свои знания
(a) Добавьте 2.334 мл и 0,31 мл.
(b) Вычтем 55,8752 м из 56,533 м.
Ответ:
(а) 2,64 мл; (б) 0,658 м
Пример 3
Умножение и деление со значащими числами
Правило: когда мы умножаем или делим числа, мы должны округлять результат до того же числа цифр, что и число с наименьшим числом значащих цифр (наименее точное значение с точки зрения умножения и разделение).
(а) Умножить 0.2 \ text {(округление до двух значащих цифр)} \\ [0.75em] \ text {четыре значащих цифры} \ times \ text {две значащих цифры} \ rightarrow \ text {ответ двух значащих цифр} [/ latex]
(b) [латекс] \ frac {421.23 \ text {g}} {486 \ text {mL}} = 0,86728 \ dots \ text {г / мл} \ rightarrow \ text {результат 0,867 г / мл (округляется до три значащих цифры)} \\ [0.75em] \ frac {\ text {пять значащих цифр}} {\ text {три значащих цифры}} \ rightarrow \ text {ответ трех значащих цифр} [/ latex]
Проверьте свои знания
(a) Умножьте 2.334 см и 0,320 см.
(b) Разделим 55,8752 м на 56,53 с.
Ответ:
(а) 0,747 см 2 (б) 0,9884 м / с
Среди всех этих технических деталей важно помнить о причине, по которой мы используем значащие числа и правила округления, — чтобы правильно представить достоверность значений, которые мы сообщаем, и гарантировать, что вычисленный результат не будет представлен как нечто большее. определенно, чем наименее определенное значение, используемое в расчетах.
Пример 4
Расчет со значащими цифрами
Одна обычная ванна — 13.3, \; \ text {или} \; 202 \ text {L (ответ с округлением до трех значащих цифр)} \ end {array} [/ latex]
Проверьте свои знания
Какова плотность жидкости с массой 31,1415 г и объемом 30,13 см 3 ?
Пример 5
Экспериментальное определение плотности с использованием вытеснения водой
Кусок арматурного стержня взвешивается и затем погружается в градуированный цилиндр, частично заполненный водой, с полученными результатами, как показано.3 [/ латекс]
(округлено до двух значащих цифр согласно правилу умножения и деления)
Из таблицы 4 в главе 1.4 «Измерения», плотность железа составляет 7,9 г / см 3 , что очень близко к плотности арматуры, что подтверждает тот факт, что арматура в основном состоит из железа.
Проверьте свои знания
Кусок блестящего желтоватого материала неправильной формы взвешивают, а затем погружают в градуированный цилиндр с полученными результатами, как показано.
(a) Используйте эти значения для определения плотности этого материала.
(b) Есть ли у вас какие-либо разумные предположения относительно идентичности этого материала? Объясните свои рассуждения.
Ответ:
(а) 19 г / см 3 ; (б) Вероятно, золото; правильного внешнего вида для золота и очень близкой к плотности, указанной для золота в таблице 4 в главе 1.4 «Измерения».
Ученые обычно проводят многократные измерения количества, чтобы убедиться в качестве своих результатов и знать как точность , так и точность своих результатов.Измерения считаются точными, если они дают очень похожие результаты при повторении одним и тем же способом. Измерение считается точным, если оно дает результат, очень близкий к истинному или принятому значению. Точные значения согласуются друг с другом; точные значения согласуются с истинным значением. Эти характеристики могут быть распространены на другие контексты, такие как результаты соревнований по стрельбе из лука (рис. 2).
Рис. 2. (a) Эти стрелки расположены близко как к мишени, так и друг к другу, поэтому они точны и точны.(b) Эти стрелки расположены близко друг к другу, но не в цель, поэтому они точны, но не точны. (c) Эти стрелы не попадают ни в цель, ни рядом друг с другом, поэтому они неточны или точны.
Предположим, химику по контролю качества в фармацевтической компании поручено проверить точность и точность работы трех разных машин, которые предназначены для выдачи 10 унций (296 мл) сиропа от кашля в бутылки для хранения. Она продолжает использовать каждую машину для наполнения пяти бутылок, а затем тщательно определяет фактический выданный объем, получая результаты, приведенные в таблице 5.
| Диспенсер # 1 | Диспенсер # 2 | Диспенсер # 3 |
|---|---|---|
| 283,3 | 298,3 | 296,1 |
| 284,1 | 294,2 | 295,9 |
| 283,9 | 296,0 | 296,1 |
| 284,0 | 297,8 | 296,0 |
| 284,1 | 293,9 | 296,1 |
| Таблица 5. Объем (мл) лекарства от кашля, выдаваемый дозаторами на 10 унций (296 мл) | ||
Принимая во внимание эти результаты, она сообщит, что дозатор № 1 является точным (все значения близки друг к другу, в пределах нескольких десятых миллилитра), но неточным (ни одно из значений не приближается к целевому значению 296 мл. , каждый из которых более чем на 10 мл меньше). Результаты для дозатора № 2 показывают повышенную точность (каждый объем меньше 3 мл от 296 мл), но худшую точность (объемы различаются более чем на 4 мл).Наконец, она может сообщить, что дозатор № 3 работает нормально, дозируя сироп от кашля точно (все объемы в пределах 0,1 мл от заданного объема) и точно (объемы отличаются друг от друга не более чем на 0,2 мл).
Количества могут быть точными или измеренными. Измеренные величины имеют связанную неопределенность, которая представлена количеством значащих цифр в измерении. Неопределенность вычисленного значения зависит от неопределенностей значений, используемых в расчетах, и отражается в том, как значение округляется.Измеренные значения могут быть точными (близкими к истинному значению) и / или точными (с небольшими отклонениями при повторных измерениях).
Химия: упражнения в конце главы
- Выразите каждое из следующих чисел в экспоненциальном представлении с правильными значащими цифрами:
(а) 711.0
(б) 0,239
(в)
(г) 134,2
(д) 0,05499
(ж) 10000,0
(г) 0,000000738592
- Выразите каждое из следующих чисел в экспоненциальной записи с правильными значащими цифрами:
(а) 704
(б) 0.03344
(в) 547.9
(г) 22086
(д) 1000.00
(ж) 0,0000000651
(г) 0,007157
- Укажите, можно ли точно определить каждое из следующего или необходимо ли его измерить с некоторой степенью неопределенности:
(а) количество яиц в корзине
(б) масса десятка яиц
(c) количество галлонов бензина, необходимое для заправки автомобильного бензобака
(г) количество см в 2 м
(е) масса учебника
(f) время, необходимое для поездки из Сан-Франциско в Канзас-Сити со средней скоростью 53 миль / ч
- Укажите, можно ли точно определить каждое из следующего или необходимо ли его измерить с некоторой степенью неопределенности:
(а) количество секунд в часе
(б) количество страниц в этой книге
(c) количество граммов в вашем весе
(d) количество граммов в 3 килограммах
(e) объем воды, который вы выпиваете за день
(f) расстояние от Сан-Франциско до Канзас-Сити
- Сколько значащих цифр содержится в каждом из следующих измерений?
(а) 38.7 г
(б) 2 × 10 18 м
(в) 3 486 002 кг
(г) 9.74150 × 10 −4 Дж
(д) 0,0613 см 3
(ж) 17,0 кг
(г) 0,01400 г / мл
- Сколько значащих цифр содержится в каждом из следующих измерений?
(а) 53 см
(б) 2,05 × 10 8 м
(в) 86 002 Дж
(г) 9,740 × 10 4 м / с
(д) 10,0613 м 3
(ж) 0.17 г / мл
(г) 0,88400 с
- Следующие количества были указаны на этикетках коммерческих продуктов. Определите количество значащих цифр в каждой.
(а) 0,0055 г действующие вещества
(б) 12 таблеток
(в) 3% перекись водорода
(d) 5,5 унций
(д) 473 мл
(ж) 1,75% висмута
(г) 0,001% фосфорная кислота
(ч) 99,80% инертных ингредиентов
- Округлите каждое из следующих чисел до двух значащих цифр:
(а) 0.436
(б) 9.000
(в) 27,2
(г) 135
(д) 1.497 × 10 −3
(ж) 0,445
- Округлите каждое из следующих чисел до двух значащих цифр:
(а) 517
б) 86,3
(в) 6.382 × 10 3
(г) 5.0008
(д) 22,497
(ж) 0,885
- Выполните следующие вычисления и запишите каждый ответ с правильным количеством значащих цифр.
(а) 628 × 342
(б) (5,63 × 10 2 ) × (7,4 × 10 3 )
(c) [латекс] \ frac {28.0} {13.483} [/ латекс]
(г) 8119 × 0,000023
(д) 14,98 + 27,340 + 84,7593
(ж) 42,7 + 0,259
- Выполните следующие вычисления и запишите каждый ответ с правильным количеством значащих цифр.
(а) 62,8 × 34
(б) 0,147 + 0,0066 + 0,012
(в) 38 × 95 × 1,792
(г) 15 — 0.15 — 0,6155
(e) [латекс] 8,78 \ times (\ frac {0,0500} {0,478}) [/ латекс]
(ж) 140 + 7,68 + 0,014
(г) 28,7 — 0,0483
(h) [латекс] \ frac {(88,5-87,57)} {45,13} [/ латекс]
- Рассмотрим результаты соревнований по стрельбе из лука, показанные на этом рисунке.
(a) Какой лучник самый точный?
(b) Какой лучник самый точный?
(c) Кто наименее точен и наименее точен?
- Классифицируйте следующие наборы измерений как точные, точные, и то, и другое, или ни одно из них.
(a) Проверка однородности веса шоколадного печенья: 17,27 г, 13,05 г, 19,46 г, 16,92 г
(b) Проверка объема партии пипеток на 25 мл: 27,02 мл, 26,99 мл, 26,97 мл, 27,01 мл
(c) Определение чистоты золота: 99,9999%, 99,9998%, 99,9998%, 99,9999%
Глоссарий
- точность
- насколько точно измерение соответствует правильному значению
- точное число
- число, полученное путем подсчета или по определению
- точность
- насколько точное измерение соответствует тому же измерению при повторении
- округление
- процедура, используемая для обеспечения того, чтобы результаты расчетов должным образом отражали неопределенность измерений, использованных в расчетах
- значащих цифр
- (также значащие цифры) все измеренные цифры в определении, включая неопределенную последнюю цифру
- неопределенность
- оценка суммы, на которую измерение отличается от истинного значения
Решения
Ответы к упражнениям в конце главы по химии
2.(а) 7,04 × 10 2 ; (б) 3,344 × 10 −2 ; (в) 5,479 × 10 2 ; (г) 2,2086 × 10 4 ; (e) 1,00000 × 10 3 ; (е) 6,51 × 10 −8 ; (ж) 7,157 × 10 −3
4. (а) точное; (б) точный; (c) неопределенный; (г) точный; (e) неопределенный; (f) неопределенный
6. (a) два; (б) три; (c) пять; (г) четыре; (д) шесть; (е) два; (г) пять
8. (а) 0,44; (б) 9,0; (c) 27; (d) 140; (д) 1,5 × 10 −3 ; (е) 0,44
10.(а) 2,15 × 10 5 ; (б) 4,2 × 10 6 ; (c) 2,08; (d) 0,19; е) 27 440; (е) 43,0
12. (a) Арчер X; (б) Арчер В; (c) Лучник Y
Accuracy and Precision Chemistry Tutorial
Пожалуйста, не блокируйте рекламу на этом сайте.
Нет рекламы = нам нет денег = нет бесплатных вещей для вас!
Точность
Точность описывает соответствие между определенным значением и истинным значением .
Пример: Известно, что истинное значение массы куба железа равно 7.90 г .
Вы весите тот же кубик железа, и определяет, что имеет массу 7,90 г .
Определенное значение и истинное значение одинаковы, поэтому может сказать , что мы точно определили массу железного куба.
Пример: вы взвешиваете тот же кубик железа на других электронных весах и на этот раз определяете, что масса железного куба равна 5.78 г .
Определенное значение сильно отличается от истинного значения , поэтому не может сказать , что мы точно определили массу железного куба.
Мы говорим, что полученное значение массы железного куба неточно.
Говоря о точности измерения, химики хотят знать, насколько точны измерения.
По этой причине мы вычисляем относительную погрешность в процентах, как показано ниже:
| относительная погрешность в процентах | = | истинное значение — определенное значение истинное значение | × 100 |
Для точного измерения относительная погрешность в процентах будет очень низкой, близкой к 0%.
В случае неточного измерения относительная погрешность в процентах будет высокой, например, более 5%.
Пример. Известно, что истинное значение массы куба железа составляет 7,90 г .
Железный куб взвешивается на 4 различных электронных весах, и относительная погрешность в процентах рассчитывается для каждого измерения, как показано ниже:
| Остаток | Истинное значение / г | Определенное значение / г | относительная погрешность в процентах =
| |||
|---|---|---|---|---|---|---|
| 1. | 7,90 | 7,90 |
| |||
| 2. | 7,90 | 5,78 |
| |||
| 3. | 7,90 | 7,62 |
| |||
| 4. | 7,90 | 7,58 |
|
При использовании весов 1. мы можем записать определенное нами значение как 7,90 г с относительной погрешностью 0,00%.
При использовании весов 2. мы можем записать полученное нами значение как 5,78 г с относительной погрешностью в процентах 26,8%.
Если мы знаем допуск истинного измерения, мы можем решить, что определенное значение является точным, если оно находится в пределах уровней допуска истинного измерения, и неточным, если оно выходит за пределы уровней допуска истинного значения.
Например, куб железа имеет истинное значение 7,90 ± 0,01 г истинное значение находится между 7,90 — 0,01 = 7,89 г и 7,90 + 0,01 = 7,90 г.
Точно определенное значение массы железа составляет от 7,89 г до 7,91 г.
Неточно определенное значение массы железа будет меньше 7,89 г или больше 7,91 г.
Чтобы определить, насколько точным является измерение, нам нужно знать истинное значение.
Часто мы не знаем истинного значения, поэтому не можем определить, насколько точны наши результаты.
точность
Поскольку химики очень редко знают, насколько точны измерения, они проводят ряд измерений в одних и тех же условиях, пока не получат набор измерений, хорошо согласующихся друг с другом. (1)
Воспроизводимость измерения называется точностью.
Когда все измерения очень похожи, мы говорим, что определенное значение известно точно.
Если мы не можем получить очень похожие измерения, мы не можем сказать, что значение известно точно, вместо этого мы говорим, что измерения неточны.
Мы можем сделать обобщения относительно точности набора измерений, вычислив диапазон экспериментально определенных значений:
диапазон значений = наибольшее значение — наименьшее значение
Набор измерений можно охарактеризовать как точный, если диапазон значений очень мал, то есть диапазон близок к 0
Набор измерений будет описан как неточный, если диапазон значений большой, то есть диапазон не близок к 0.
Пример. Масса железного куба была измерена 3 раза в трех отдельных испытаниях с использованием весов 1, описанных выше.
Результаты показаны ниже:
| Значения массы железного куба, определяемые Весами 1, очень разнообразны. диапазон значений = наибольшее значение — наименьшее значение диапазон значений для баланса 1. = 7,90 — 6,14 = 1,76 1.76 >> 0 Весы 1. дают неточные значения массы железного куба. |
Использование весов 1. для измерения массы не дает воспроизводимых результатов.
Весы 1. не позволяют точно измерить массу.
(Весы 1. ЗАПРЕЩАЕТСЯ использовать до тех пор, пока технический специалист не отремонтирует их!)
Пример. Масса железного куба была измерена 3 раза в трех отдельных испытаниях с использованием весов 2, описанных выше.Результаты показаны ниже:
| Значения массы железного куба, определенные Balance 2, очень похожи. диапазон значений = наибольшее значение — наименьшее значение диапазон значений для баланса 2.= 5,79 — 5,77 = 0,02 0,02 и приблизительно; 0 Весы 2. показывают точные значения массы железного куба. |
Использование весов 2. для измерения массы действительно дает воспроизводимые результаты.
Весы 2. обеспечивают точное измерение массы.
Примеры точности и прецизионности
Точность описывает соответствие между определенным значением и истинным значением.
Точность описывает воспроизводимость измерения.
Таким образом, измерения можно описать как одно из следующих:
- точный и точный
- точный, но неточный
- неточно, но точно
- неточно и неточно
Пример 1. Известно, что температура в лаборатории постоянна 25.23 ° С.
Учащийся трижды измеряет температуру в лаборатории спиртовым термометром и записывает значения температуры в приведенную ниже таблицу:
| Испытание 1 | Испытание 2 | Испытание 3 | |
|---|---|---|---|
| Зарегистрированная температура / ° C | 23,88 | 23,91 | 23,24 |
Как бы вы описали точность и точность записанных учеником температуры?
Решение:
- Определение точности результатов учащегося.
Чтобы определить точность, нам нужно сравнить каждый из результатов ученика с истинным значением, заданным как 25,23 o C.
Учитывая, что у нас есть несколько различных измерений с использованием одного и того же термометра, выполненных студентом в одной и той же лаборатории, мы могли бы начать с усреднения результатов студента:средняя зарегистрированная температура = 23,88 + 23,91 + 23,24
3= 71.03
3= 23,68 Затем мы можем использовать это среднее значение для вычисления относительной погрешности в процентах, позволяя средней зарегистрированной температуре быть определенным значением:
относительная погрешность в процентах = истинное значение — определенное значение
истинное значение× 100 относительная погрешность в процентах = 25.23-23,68
25,23× 100 относительная погрешность в процентах = 6,14% Определенное значение является точным, если относительная погрешность в процентах низкая, близкая к 0%.
Относительная ошибка в результатах ученика НЕ близка к 0%.
Показания температуры учащегося НЕ точны, они неточны. - Определение точности результатов ученика.
Набор измерений является точным, если все измерения очень похожи, то есть если имеется небольшой диапазон значений.
Найдите диапазон показаний термометра студента:
самая высокая зарегистрированная температура 23,91 ° C
самая низкая зарегистрированная температура 23,24 ° Cдиапазон значений = наибольшее значение — наименьшее значение = 23.91 — 23,24 = 0,67
Диапазон значений ближе к 1, чем к 0, поэтому мы можем решить, что измерения ученика НЕ точны, они неточны. - Заключение: показания температуры ученика неточны и неточны.
Показания температуры учащегося неточны и неточны.
Пример 2. Известно, что объем воды в мерной колбе равен 50.00 ± 0,06 мл при 20 ° C и 101,3 кПа.
Студент с помощью мерного цилиндра на 100 мл трижды измеряет объем воды в колбе.
Результаты ученика занесены в таблицу ниже:
| Испытание 1 | Испытание 2 | Испытание 3 | |
|---|---|---|---|
| Зарегистрированный объем / мл | 49,84 | 49,92 | 49,91 |
Как бы вы описали точность записанных учеником объемов воды?
Решение:
- Определение точности результатов учащегося.
Чтобы определить точность, нам нужно сравнить каждый из результатов ученика с истинным значением, равным 50,00 ± 0,06 мл.
Учитывая, что у нас есть несколько различных измерений с использованием одного и того же мерного цилиндра, выполненного одним и тем же студентом в одной лаборатории, мы могли бы начать с усреднения результатов студента:средний зарегистрированный объем воды = 49,84 + 49,92 + 49,91
3= 149.



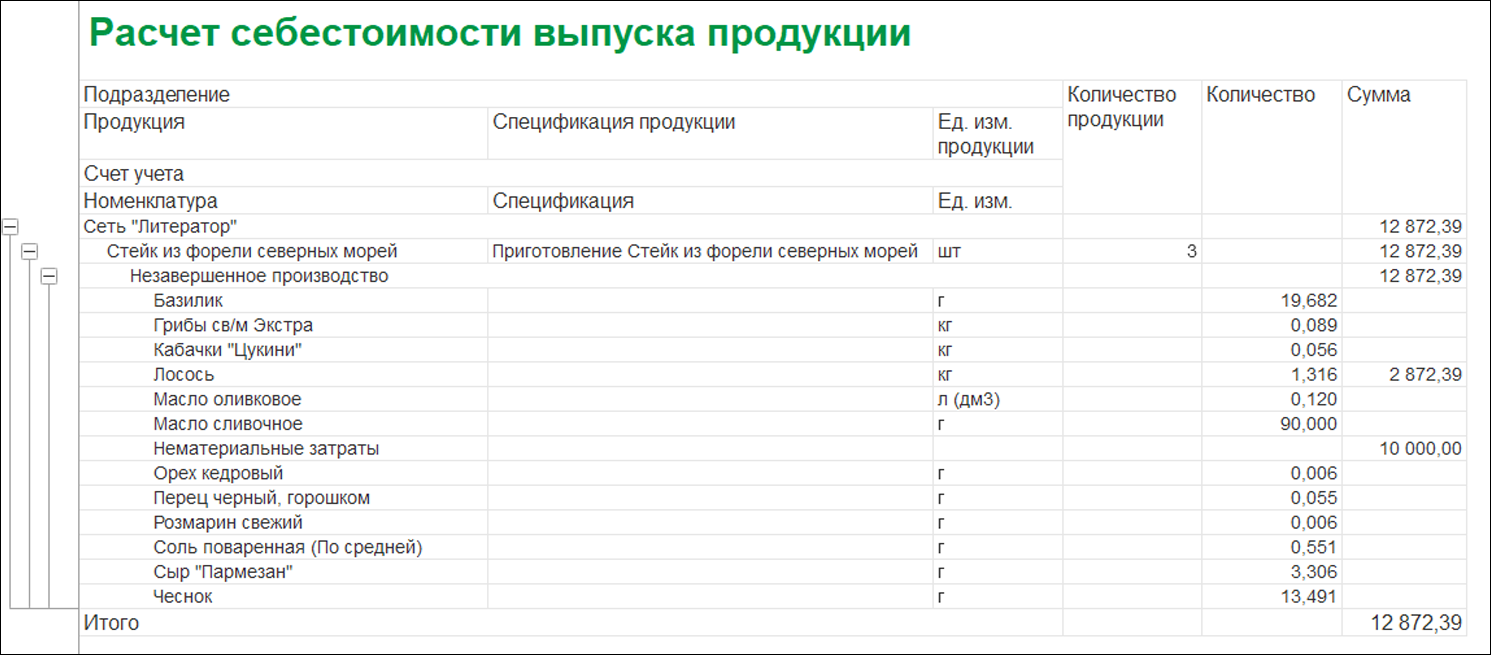 Страхователь имеет право установить индивидуальную ставку разным водителям, чьи средства передвижения были зарегистрированы на одной территории. При этом главной величиной в установлении тарификации является грубое нарушение ПДД.
Страхователь имеет право установить индивидуальную ставку разным водителям, чьи средства передвижения были зарегистрированы на одной территории. При этом главной величиной в установлении тарификации является грубое нарушение ПДД. Равняется 1 в случае, если в договоре указаны определенные водители, если они не вписаны, стоимость страхования увеличивается вдове;
Равняется 1 в случае, если в договоре указаны определенные водители, если они не вписаны, стоимость страхования увеличивается вдове;
 "Применить скидку на вакансию" THEN
"Применить скидку на вакансию" THEN 