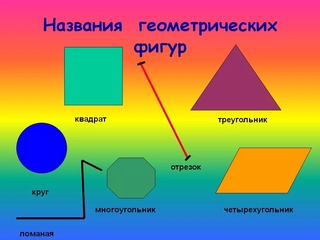
Фигуры название: Основные геометрические фигуры 🟢🟨🔺 и их названия
Основные геометрические фигуры
Каждый из нас — и взрослый, и ребенок — замечал, как много геометрических фигур существует вокруг нас. Мы встречаемся с ними везде, во всех окружающих нас предметах. Где же встречаются геометрические фигуры в нашей жизни?
Где встречаются геометрические фигуры в нашей жизни?
Каждый из нас — и взрослый, и ребенок — замечал, как много геометрических фигур существует вокруг нас. Мы встречаемся с ними везде, во всех окружающих нас предметах.
Люди давно заинтересовались разнообразием геометрических фигур. Ещё для первобытных людей важную роль играла форма окружавших их предметов. Овладевая миром, люди знакомились с простейшими геометрическими формами. Сначала они изготавливали орудия труда относительно правильной формы, потом научились их совершенствовать. Специальных названий для геометрических фигур тогда, конечно, не было. Их придумали значительно позже. Когда люди стали строить дома, им пришлось ещё глубже разбираться в особенностях разных фигур, чтобы понять, какую форму следует придавать стенам и крыше, какой формы должны быть брёвна или каменные глыбы. Сам того не зная, человек всё время занимался изучением фигур: женщины, изготавливая одежду, охотники — наконечники для копий или бумеранги сложной формы, рыболовы, делая такие крючки из кости, чтобы рыба с них не срывалась.
Сам того не зная, человек всё время занимался изучением фигур: женщины, изготавливая одежду, охотники — наконечники для копий или бумеранги сложной формы, рыболовы, делая такие крючки из кости, чтобы рыба с них не срывалась.
И в современном мире без этих знаний не прожить.
Где же встречаются геометрические фигуры в нашей жизни?
Возможно, кто-то считает, что различные линии фигуры «водятся» только в книгах учёных математиков. Однако, если посмотреть вокруг, становится понятно, что многие предметы имеют форму, похожую на основные геометрические фигуры. Просто мы не всегда это замечаем. Немало замечательных геометрических фигур встречается в окружающей нас природе. Поле имеет форму прямоугольника, река — кривой линии, озеро — круга, кристалл соли — форму куба, обычная горошинка, капелька росы — форму шара. Красивы и разнообразны многогранники — кристаллы горного хрусталя. Но и в привычной жизни основные геометрические фигуры тоже повсюду. Это здания, строения, транспорт, интерьер квартиры, даже посуда и предметы одежды.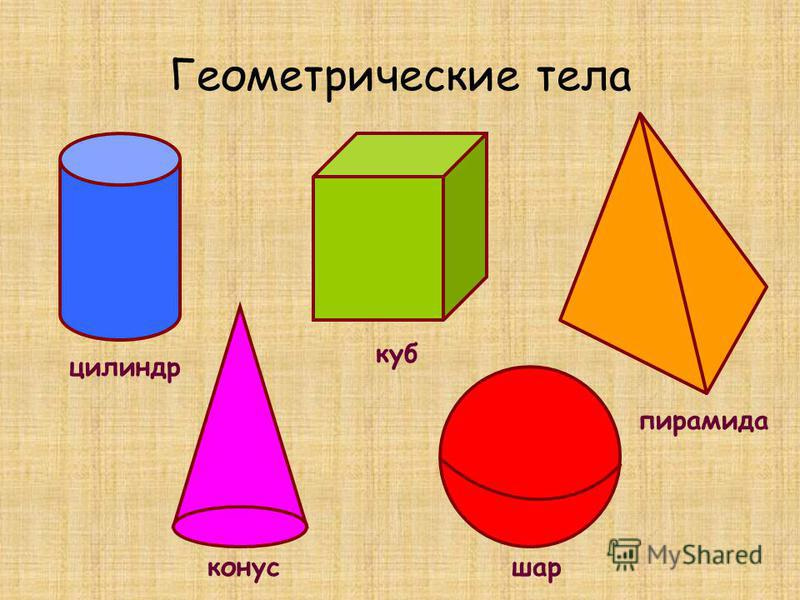 К примеру, женская юбка — это трапеция, тарелка — круг, дом — квадрат и треугольник, а в трубе — цилиндр.
К примеру, женская юбка — это трапеция, тарелка — круг, дом — квадрат и треугольник, а в трубе — цилиндр.
Знать все фигуры, их виды, названия и свойства очень важно. Систематизирует знания о геометрических фигурах и изучает их свойства математическая наука — геометрия. Наука эта очень важная, её применение просто бесценно во все времена и независимо от профессии. Без знаний геометрии не обходится ни рабочий, ни инженер, ни архитектор, ни художник. И очень важно начать осваивать эту науку в раннем возрасте.
Прекрасным помощником ребёнку в этом станет образовательная платформа iSmart. Основные виды геометрических фигур, их свойства, задачи на нахождение площади фигур и многое другое есть на платформе в разделе «Математика». Тут собраны несколько тысяч заданий на освоение этих тем, не повторяющиеся при многократной отработке. Занимаясь на , школьники начальных классов досконально разберутся в основах геометрии. Это даст им хорошую базу по предмету для учёбы в средних и старших классах.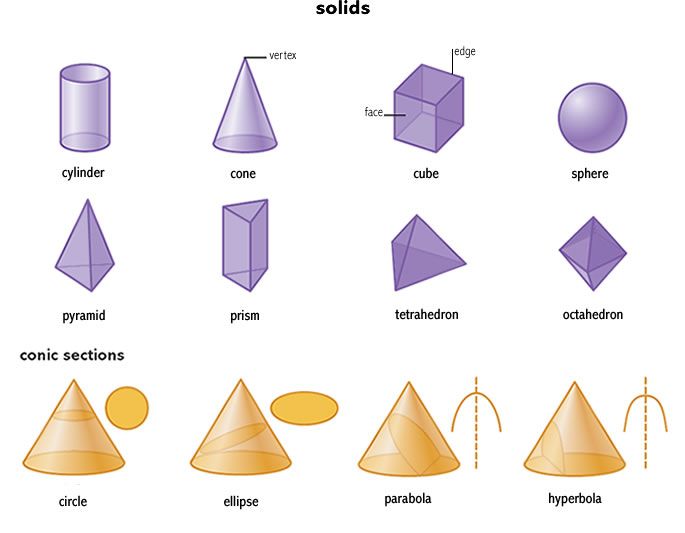 Кроме того, интерактивные задания красочные, интересные, увлекательные.
Кроме того, интерактивные задания красочные, интересные, увлекательные.
Итак,
Простейшие виды фигур
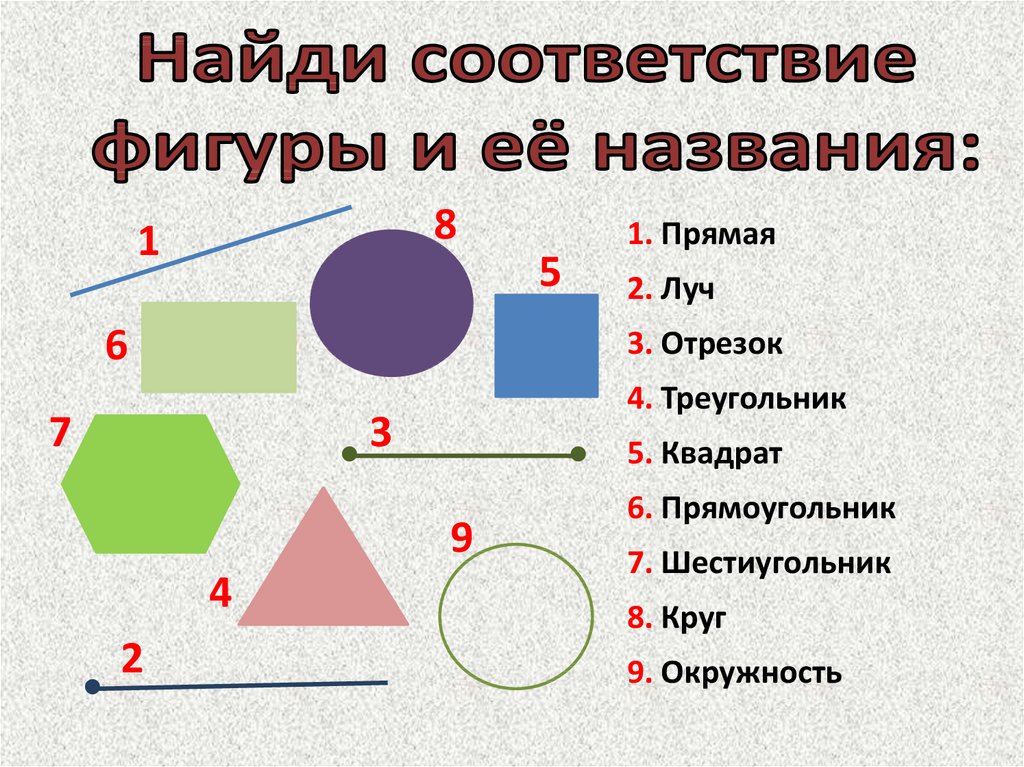
Две основные фигуры — это точка и линия. Скопление точек и линий образует различные геометрические фигуры. Каждая из них индивидуальна, отличается своими параметрами, их формы очень разнообразны. Фигуры бывают простыми и сложными, плоскими и объёмными.
Точка
Точка — это самый минимальный, но в то же время самый главный объект в геометрии. Это самая малая геометрическая фигура, но именно она необходима для построения других фигур на плоскости и является основой для всех других фигур. Она не содержит таких свойств, как длина, высота, объём, площадь, не имеет измерительных особенностей и характеристик. Важно только то, где она расположена. Обозначается точка заглавной буквой латинского алфавита либо числом. Например, A, B, C или 1, 2, 3.
Всякая более сложная геометрическая фигура — это множество точек, которые обладают определенным свойством, характерным только для этой фигуры.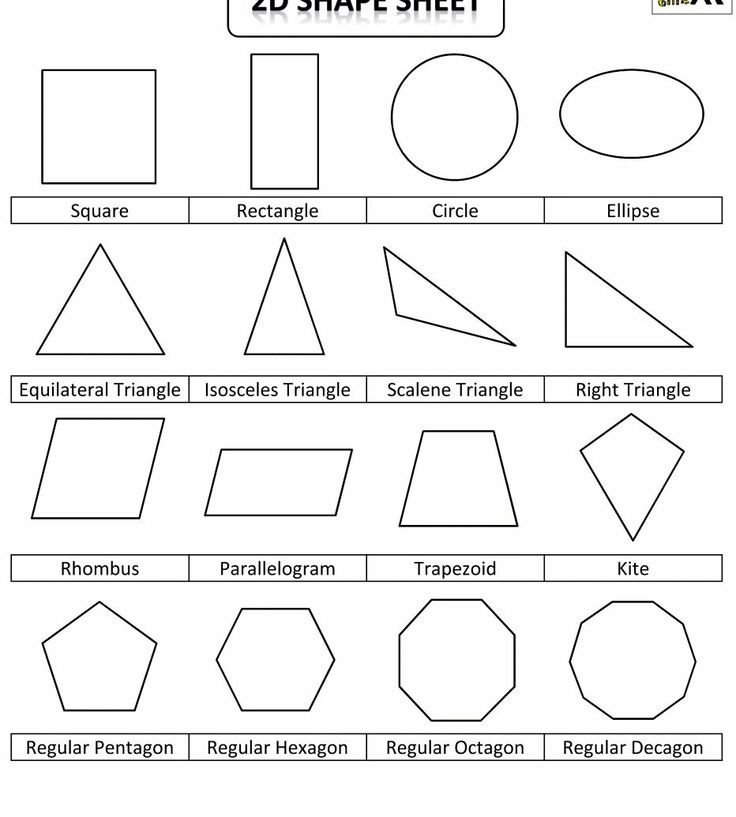
Самыми простейшими фигурами являются луч и отрезок.
- Луч — часть прямой, у которой есть начальная точка, но нет конца. Это продолжение в одну сторону.
- Отрезок — составная часть прямой, которая ограничена двумя точками. Он имеет начало и конец, поэтому измеряется. Длину отрезка можно определить, измерив расстояние между его концами.
Линия
Линия образуется из множества точек, последовательно расположенных друг за другом и соединённых между собой. Линии бывают замкнутыми и разомкнутыми, прямыми и кривыми, а также ломаными.
- Замкнутая — когда в одной точке расположена начальная и конечная часть направления. Из незамкнутой линии получают обратный вариант.
- Разомкнутая — когда начало и окончание линии не соединены.
- Прямая — непрерывная линия без изменений.

- Кривая — отличная от прямой линии.
- Ломаная — когда соединены отрезки не под углом 180 градусов.
Через одну точку можно провести бесконечное число линий, а через две — только одну прямую и множество кривых.
Основные геометрические фигуры
Соединённые между собой точки образуют линии, а соединённые между собой линии — основные геометрические фигуры на плоскости.
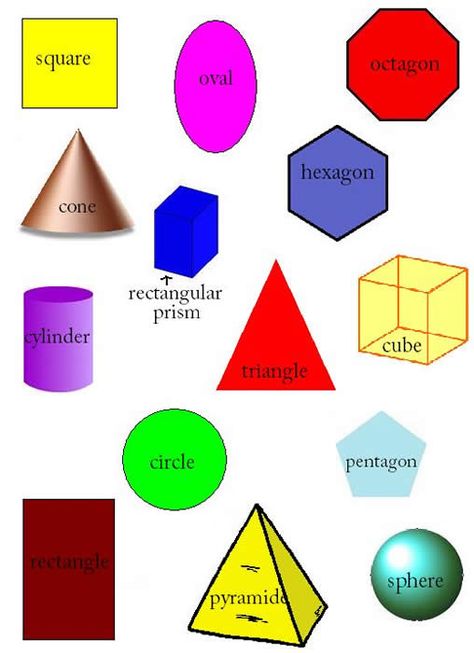
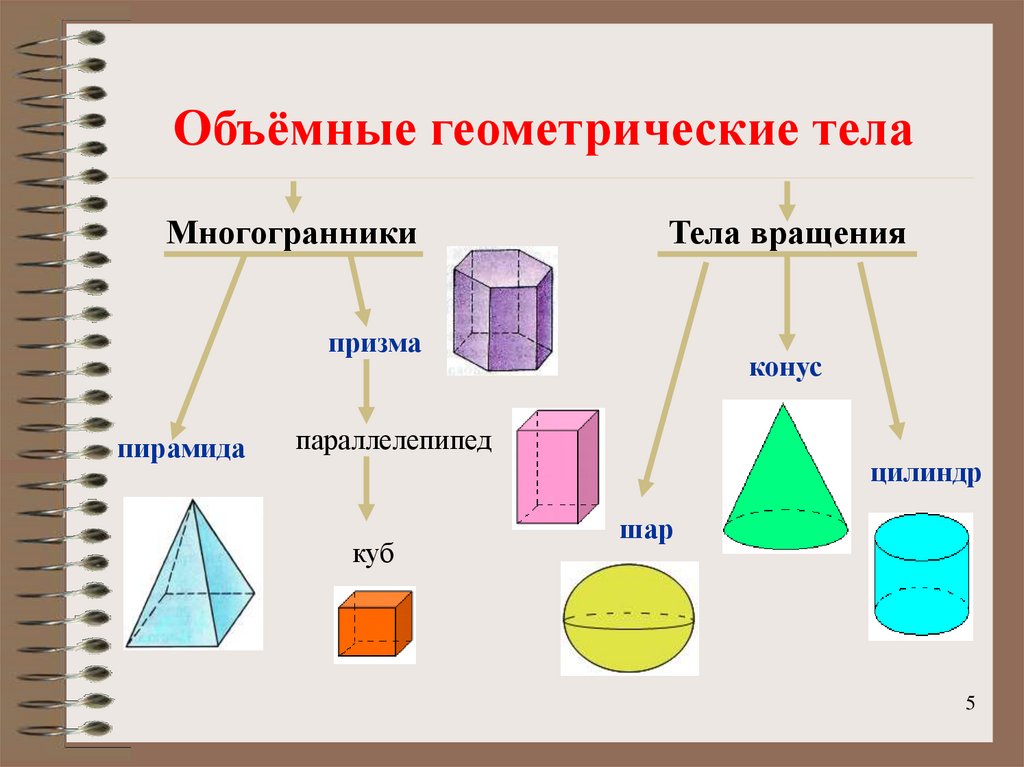
Геометрические фигуры бывают плоские или двухмерные (2D) и объёмные пространственные, или трёхмерные (3D). Они ограничены замкнутой поверхностью своей наружной границы.
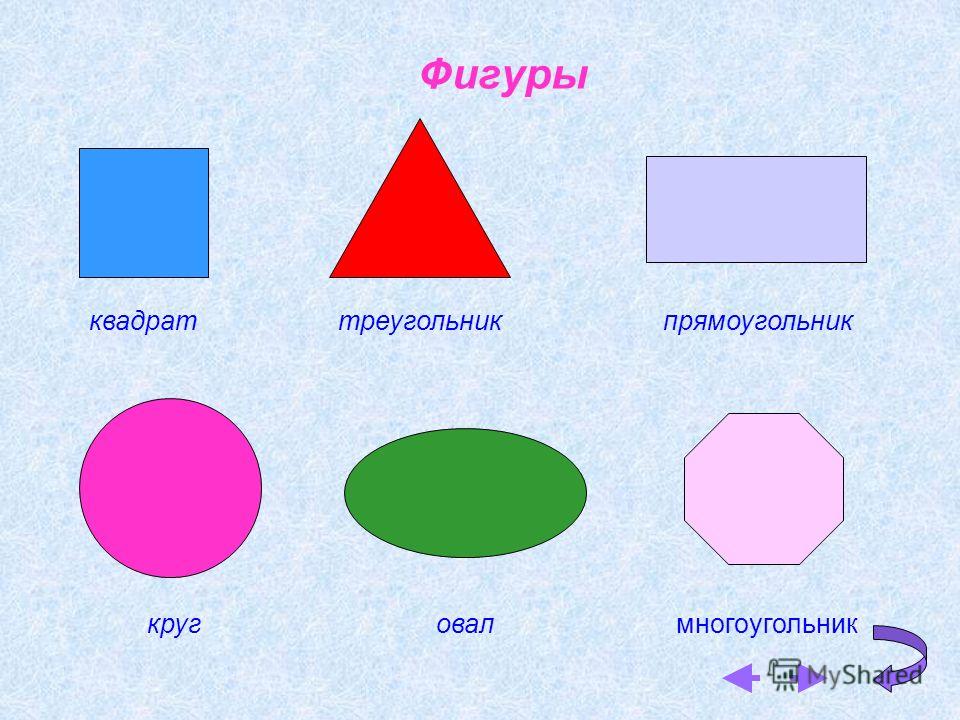
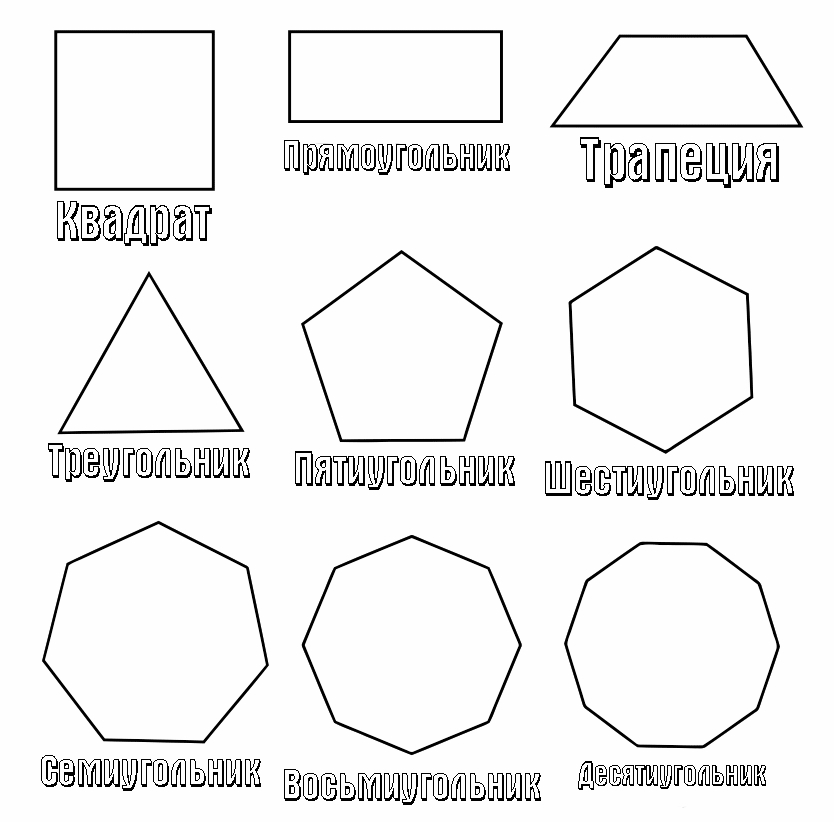
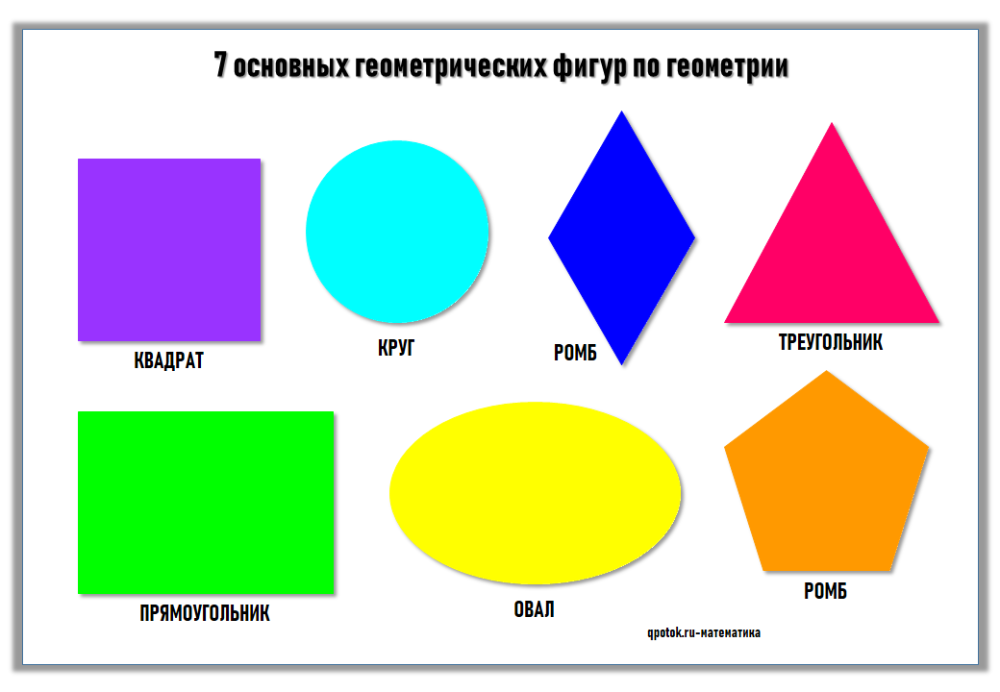
Если все точки фигуры находятся в одной плоскости, значит, она является плоской. Плоские фигуры, которые знают все: точка, квадрат, прямоугольник, треугольник, круг, полукруг, окружность, овал, ромб, трапеция.
А если у геометрической фигуры все точки не находятся в одной плоскости, то она объёмная. К ним относятся шар, конус, цилиндр, сфера, пирамида и др.
Разберём плоские фигуры.
Треугольник
Треугольник — это фигура, которая образуется, когда три отрезка соединяют три точки, не лежащие на одной прямой. Эти три точки называются вершинами, а отрезки — сторонами.
Есть три вида треугольников:
- Прямоугольный — когда один угол прямой, другие два меньше 90 градусов.
- Остроугольный — когда градус его углов больше 0, но меньше 90 градусов.
- Тупоугольный — когда один угол тупой, то есть больше 90 градусов, а два других — острые.
Треугольники имеют следующие свойства:
- в треугольнике напротив большего угла лежит большая сторона и наоборот;
- сумма углов треугольника всегда равна 180 градусам;
- все углы равностороннего треугольника равны 60 градусам;
- в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов (но это изучается уже в старших классах).

Вершины треугольников обозначаются заглавными буквами латинского алфавита: A, B, C и др.
Примеры треугольников:
Окружность
Окружность — геометрическая фигура, образованная замкнутой кривой линией, все точки которой находятся на одинаковом от центра расстоянии.
Круг
Часть плоскости, находящаяся внутри окружности, называется кругом. То есть, окружность — это граница круга. А расстояние от центра окружности до любой точки на ней называется радиусом. Диаметр круга — это отрезок, который соединяет две точки на окружности и проходит через её центр. Диаметр круга равен двум его радиусам.
Прямоугольник
Прямоугольник — это фигура, состоящая из четырёх сторон и четырёх прямых углов, у которой:
- противоположные стороны равны между собой;
- диагонали равны и делятся в точке пересечения пополам;
- около прямоугольника можно описать окружность с центром в точке пересечения его диагоналей и радиусом, который равен половине диагоналей.

Квадрат
Квадрат — это тот же прямоугольник, у которого:
- все стороны равны;
- все углы равны и составляют 90 градусов;
- диагонали равны и перпендикулярны;
- центры вписанной и описанной окружности совпадают и находятся в точке пересечения его диагоналей.
Трапеция
Четырёхугольник, у которого две стороны параллельны, а две — нет, называется трапецией. Если сумма длин оснований трапеции равна сумме длин боковых сторон, в неё можно вписать окружность.
Параллелограмм и ромб
Параллелограмм — четырёхугольник, противоположные стороны которого попарно параллельны.
Ромб — это параллелограмм с равными сторонами.
Параллелограмм имеет следующие свойства:
- противоположные стороны и углы равны;
- сумма двух любых соседних углов равна 180 градусам;
- диагонали пересекаются и точкой пересечения делятся пополам;
- каждая диагональ делит фигуру на два равных треугольника.

Основные величины и их формулы
Все геометрические фигуры имеют свои характеристики и собственную величину. Самыми распространёнными являются такие величины как площадь и периметр. Они используются в повседневной жизни, в строительстве и в других областях. Например, во время ремонта или нового строительства, количество необходимых материалов и объём работ не определить, не вычислив заранее площадь и периметр.
Периметр
Периметром называется замкнутая граница плоской геометрической фигуры, которая отделяет её внутреннюю область от внешней. Периметр есть у любой замкнутой геометрической фигуры:
На рисунке периметры выделены красной линией. Периметр окружности часто называют длиной.
Периметр измеряется в единицах измерения длины: мм, см, дм, м, км.
Обозначается заглавной латинской P.
Площадь
Площадь — это часть плоскости, занимаемая замкнутой плоской геометрической фигурой, то есть та часть плоскости, которая находится внутри периметра. Именно она даёт нам основную информацию о её размере. Любая плоская замкнутая геометрическая фигура имеет определённую площадь.
Именно она даёт нам основную информацию о её размере. Любая плоская замкнутая геометрическая фигура имеет определённую площадь.
На рисунке площади фигур окрашены различными цветами.
Измерить площадь фигуры — значит найти, сколько раз в данной фигуре помещается другая фигура, принятая за единицу измерения. Площадь измеряется в квадратных единицах измерения длины. К единицам измерения площади относятся: мм2, см2, м2, км2 и т. д. S (square) — знак площади.
Вычисление периметра и площади
Периметр — это длина замкнутого контура геометрической фигуры. Можно, конечно, измерить линейкой длины всех сторон и сложить их. Но лучше воспользоваться специальными формулами для вычисления периметра, это значительно упростит задачу.
- Квадрат: периметр = 4 * сторона.
- Треугольник: периметр = сторона 1 + сторона 2 + сторона 3.
- Неправильный многоугольник: периметр = сумме всех сторон многоугольника.

- Круг: длина окружности = 2 * π * радиус = π * диаметр (где π – это число пи (константа, примерно равная 3,14), радиус – это длина отрезка, соединяющего центр окружности и любую точку, лежащую на этой окружности, диаметр – это длина отрезка, проходящего через центр окружности и соединяющего любые две точки, лежащие на этой окружности).
Для вычисления площади фигуры также потребуется соответствующая формула. К разным фигурам применяются разные формулы. Для вычисления площади стандартных геометрических фигур можно воспользоваться следующими формулами:
- Параллелограмм: площадь = основание * высота
- Квадрат: площадь = сторона 1 * сторона 2
- Треугольник: площадь = ½ * основание * высота
- Круг: площадь = π * радиус² (где радиус – это длина отрезка, соединяющего центр окружности и любую точку, лежащую на этой окружности. Квадрат радиуса – это значение радиуса, умноженное само на себя).

Итак, мы перечислили основные и самые распространённые геометрические фигуры и их свойства. Образовательная платформа iSmart поможет вашему ребёнок изучить основные геометрические фигуры, их виды, названия и свойства с помощью увлекательных заданий. Преимущества занятий на умных тренажёрах iSmart:
- интерактивные задания больше похожи на игру;
- их можно отрабатывать многократно и они не будут повторяться;
- платформа сформирует индивидуальную траекторию обучения на основе диагностики знаний;
- достаточно всего 20 минут занятий в день, чтобы в короткий срок увидеть прогресс в обучении.
Кроме того, занятия помогут вам освободить своё время, ведь ребёнок сможет заниматься самостоятельно, а родитель — получать отчёты и наблюдать за динамикой обучения. Метод обучения iSmart основан на последних научных практиках: микрообучение и поведенческий анализ.
Образовательная платформа iSmart предлагает подготовку к контрольным работам, тестам, ВПР, олимпиадам, а также изучение дополнительных предметов, не вошедших в школьную программу.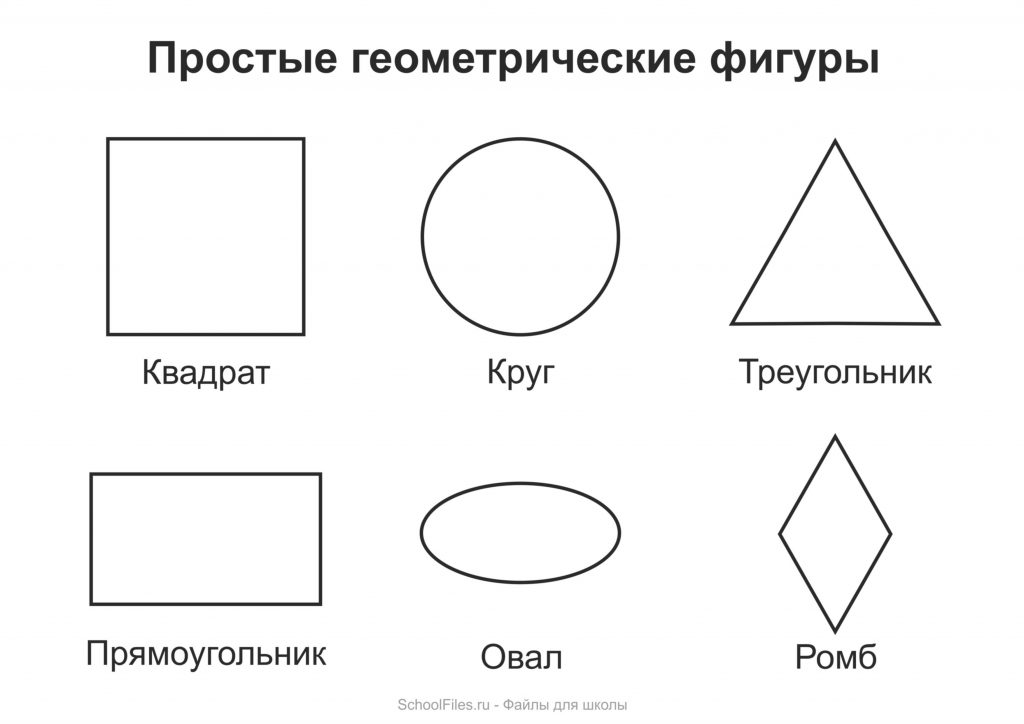
Названия геометрических фигур . Математика для мам и пап: Домашка без мучений
Правильные геометрические фигуры – треугольники, квадраты, пятиугольники и т. д. – фигурируют в математике со времен древних греков. Этим объясняются их названия (по крайней мере, варианты названий), семь из которых происходят непосредственно от греческих названий чисел:
Однако – наверное для того, чтобы всех нас запутать, – название правильной четырехсторонней фигуры, четырехугольника, пришло из латыни (quadratus), тогда как 9– и 11-угольники встречаются так редко, что трудно найти человека, который знал бы, как они называются (на случай, если вас это интересует, скажем, что эти названия соответственно «нонагон» и «гендекагон»).
Числа в названиях действительно указывают на количество сторон в многоугольнике, а вот «гон» – часть названия, которая произошла от греческого gonu, означающего колено; это слово начали применять в отношении углов, поскольку колено человека тоже образует угол. Фигура называется правильной, если все ее стороны одинаковой длины, а все углы равны, так что вот это, к примеру, правильный шестиугольник:
Фигура называется правильной, если все ее стороны одинаковой длины, а все углы равны, так что вот это, к примеру, правильный шестиугольник:
С другой стороны, эти два шестиугольника не являются правильными (по крайней мере в строго математическом смысле этого слова):
Фигуры с большим числом сторон, как правило, называют просто многоугольниками, или полигонами, используя приставку поли-, что означает «много».
Игра: «Я вижу… шестиугольник»
Интересные геометрические фигуры можно найти везде: в доме, на улицах, в путешествиях. Некоторые фигуры по-настоящему вездесущи. Оглянитесь вокруг – и в любом помещении вы, вероятно, без труда отыщете несколько прямоугольников и пару окружностей. С остальными фигурами сложнее. Можно превратить поиск интересных фигур в игру «Я вижу…» и давать за разные фигуры разное количество очков. Во время поездки на машине попросите детей обращать внимание на:
• Дорожные знаки и крыши, которое чаще всего треугольные.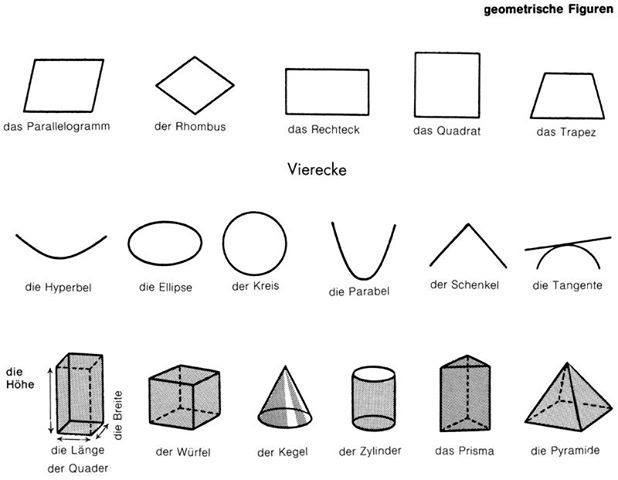 (Вообще треугольники довольно-таки трудно найти в помещениях. В качестве примеров можно привести угловые лестницы.) Стоимость: 1 очко.
(Вообще треугольники довольно-таки трудно найти в помещениях. В качестве примеров можно привести угловые лестницы.) Стоимость: 1 очко.
• Очень небольшое число предметов или зданий имеет форму пятиугольника (знаменитый американский Пентагон – редкий пример). Можно, однако, отыскать пятиугольники в предметах, если знаешь, на что обращать внимание. На большинстве футбольных мячей пятиугольники имеются (см. «Футбольный мяч и шестиугольники» в этой главе). Разрежьте яблоко поперек – и увидите пять ячеек с семечками, образующих правильный пятиугольник. Разрежьте поперек неочищенный банан – и увидите, что в сечении он образует пятистороннюю фигуру со слегка скругленными сторонами, по существу, пятиугольник. Возьмите узкую полоску бумаги, завяжите ее в узел и осторожно расплющите. Из узла получится правильный пятиугольник (посмотрите через него на свет, чтобы разглядеть получше). Стоимость: 5 очков.
• Пчелиные соты состоят из правильных шестиугольников, но вряд ли вы каждый день изучаете внутреннее устройство пчелиных сот. Если взять игральный кубик и наклонить его так, чтобы один из углов указывал прямо на вас, то очертания кубика образуют шестиугольник. Шестиугольники имеются на большинстве футбольных мячей, а у многих стаканов для воды на кухне и в ресторанах шестиугольные донышки. Большинство карандашей представляет собой шестиугольные призмы – как и современные упаковки некоторых мелких конфет-драже. Стоимость: 4 очка.
Если взять игральный кубик и наклонить его так, чтобы один из углов указывал прямо на вас, то очертания кубика образуют шестиугольник. Шестиугольники имеются на большинстве футбольных мячей, а у многих стаканов для воды на кухне и в ресторанах шестиугольные донышки. Большинство карандашей представляет собой шестиугольные призмы – как и современные упаковки некоторых мелких конфет-драже. Стоимость: 4 очка.
• Единственными семиугольниками, которые вы встретите в обычной жизни, окажутся, скорее всего, английские монеты по 20 и 50 пенсов, представляющие собой сглаженные семиугольники. (Монеты с нечетным числом сторон имеют постоянный диаметр и потому годятся для использования в автоматах, поскольку машина может распознать края монеты, какой бы стороной она ни легла.) Стоимость: 10 баллов.
Ширина 50-пенсовой монеты остается одной и той же, какой стороной ни поверни.
• Обычный дорожный знак «СТОП» представляет собой восьмиугольник. Кроме того, восьмиугольники в сочетании с квадратами были популярным элементом дизайна викторианских каминов и выложенных плиткой дорожек, так что в Британии их иногда можно обнаружить на полу какого-нибудь учреждения (или даже жилого дома, если он достаточно стар). Эстрада, на которой играет местный любительский оркестр, скорее всего, имеет восьмиугольную форму (в принципе она может оказаться шестиугольной, но такие увидишь редко. В церквях, да и в других важных зданиях, нередко имеются пространства восьмиугольной формы – такие строения легко возводить, потому что восьмиугольник – это просто квадрат со срезанными углами. Дома стоит обратить внимание на форму всевозможных косметических тюбиков и коробочек; вероятно, среди этих предметов найдется что-нибудь восьмиугольное. Стоимость: 5 баллов.
Эстрада, на которой играет местный любительский оркестр, скорее всего, имеет восьмиугольную форму (в принципе она может оказаться шестиугольной, но такие увидишь редко. В церквях, да и в других важных зданиях, нередко имеются пространства восьмиугольной формы – такие строения легко возводить, потому что восьмиугольник – это просто квадрат со срезанными углами. Дома стоит обратить внимание на форму всевозможных косметических тюбиков и коробочек; вероятно, среди этих предметов найдется что-нибудь восьмиугольное. Стоимость: 5 баллов.
• Фигуры, у которых сторон больше восьми, встречают чрезвычайно редко. Может быть, вам удастся обнаружить их в граненом стакане или в форме какого-нибудь здания, а иногда также в иностранных монетах: канадская монета номиналом в доллар, известная как «луни», – редкий пример гендекагона (это, если вы помните, 11-угольник), а австралийские 50 центов и старый британский (еще до введения десятичной денежной системы) трехпенсовик – додекагоны (12-угольники). А на ярмарочной площади мы обнаружили настоящий 16-угольник в основании карусели. Одна из причин редкой встречаемости этих геометрических фигур заключается в том, что их форма настолько приближается к окружности, что проще сделать вещь круглой, чем устраивать канитель с многочисленными прямыми сторонами. Стоимость: 20 баллов.
А на ярмарочной площади мы обнаружили настоящий 16-угольник в основании карусели. Одна из причин редкой встречаемости этих геометрических фигур заключается в том, что их форма настолько приближается к окружности, что проще сделать вещь круглой, чем устраивать канитель с многочисленными прямыми сторонами. Стоимость: 20 баллов.
рисунков и диаграмм – Центр письма • Университет Северной Каролины в Чапел-Хилл
О чем эта брошюра
В этом руководстве рассказывается, как использовать рисунки и таблицы для представления сложной информации таким образом, чтобы она была доступна и понятна вашему читателю.
Нужен ли рисунок/таблица?
При планировании написания важно подумать о том, как лучше всего донести информацию до аудитории, особенно если вы планируете использовать данные в виде цифр, слов или изображений, которые помогут вам сформулировать и поддержать вашу аргументацию. Вообще говоря, сводки данных могут иметь форму текста, таблиц или рисунков. Большинство писателей знакомы с текстовыми сводками данных, и часто это лучший способ сообщить простые результаты. Хорошее эмпирическое правило — посмотреть, сможете ли вы четко представить свои результаты в одном-двух предложениях. Если да, то таблица или рисунок, вероятно, не нужны. Если ваши данные слишком многочисленны или сложны для адекватного описания в этом объеме, рисунки и таблицы могут быть эффективными способами передачи большого количества информации, не загромождая ваш текст. Кроме того, они служат кратким справочником для вашего читателя и могут выявить тенденции, закономерности или взаимосвязи, которые в противном случае было бы трудно понять.
Большинство писателей знакомы с текстовыми сводками данных, и часто это лучший способ сообщить простые результаты. Хорошее эмпирическое правило — посмотреть, сможете ли вы четко представить свои результаты в одном-двух предложениях. Если да, то таблица или рисунок, вероятно, не нужны. Если ваши данные слишком многочисленны или сложны для адекватного описания в этом объеме, рисунки и таблицы могут быть эффективными способами передачи большого количества информации, не загромождая ваш текст. Кроме того, они служат кратким справочником для вашего читателя и могут выявить тенденции, закономерности или взаимосвязи, которые в противном случае было бы трудно понять.
Так какая же разница между таблицей и фигурой?
Таблицы представляют собой списки чисел или текста в столбцах и могут использоваться для обобщения существующей литературы, объяснения переменных или представления формулировок вопросов опроса. Они также используются, чтобы сделать газету или статью более читабельной, удаляя числовые или перечисленные данные из текста.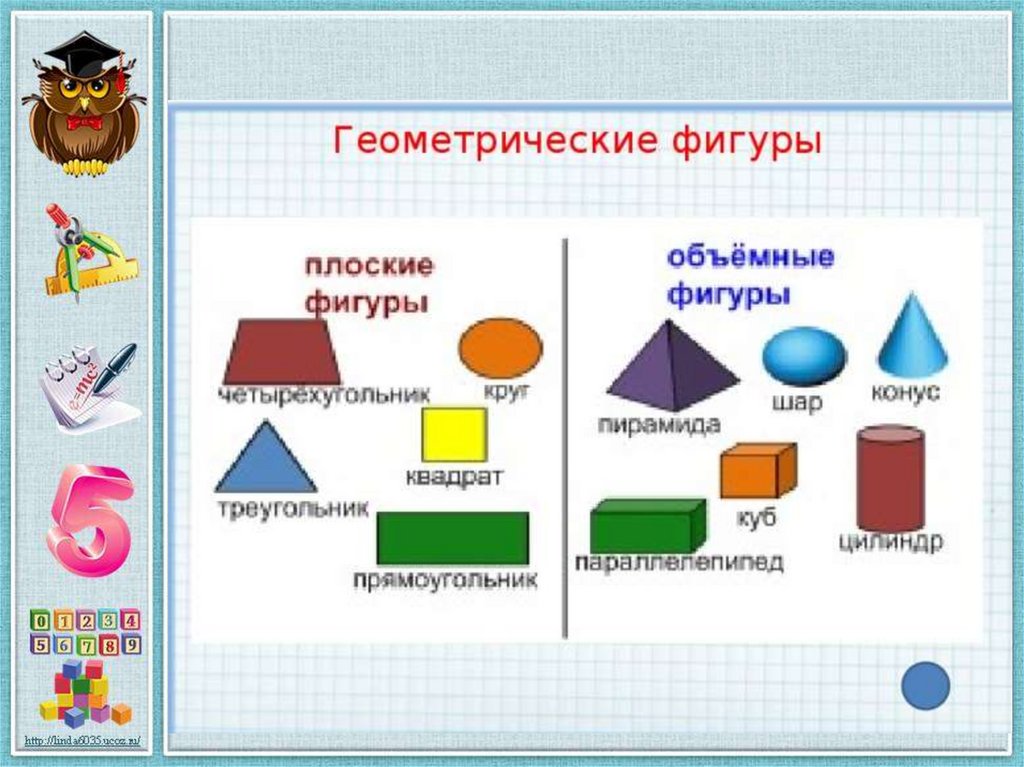 Таблицы обычно используются для представления необработанных данных, а не для отображения связи между переменными.
Таблицы обычно используются для представления необработанных данных, а не для отображения связи между переменными.
Рисунки представляют собой визуальное представление результатов. Они бывают в виде графиков, диаграмм, рисунков, фотографий или карт. Цифры обеспечивают визуальное воздействие и могут эффективно передать ваш основной вывод. Традиционно они используются для отображения тенденций и закономерностей взаимосвязей, но их также можно использовать для простого обмена информацией о процессах или отображения сложных данных. Рисунки не должны дублировать ту же информацию, что и в таблицах, и наоборот.
Использование таблиц
Таблицы легко создаются с помощью табличной функции вашего текстового процессора или программы для работы с электронными таблицами, такой как Excel. Элементы таблицы включают легенду или заголовок, заголовки столбцов и основную часть таблицы (количественные или качественные данные). Они также могут включать подзаголовки и сноски. Помните, что думать об организации таблиц так же важно, как и об организации абзацев. Хорошо организованная таблица позволяет читателям с легкостью понять смысл представленных данных, в то время как неорганизованная таблица оставит читателя в замешательстве относительно самих данных или значимости данных.
Хорошо организованная таблица позволяет читателям с легкостью понять смысл представленных данных, в то время как неорганизованная таблица оставит читателя в замешательстве относительно самих данных или значимости данных.
Заголовок: Таблицы начинаются с номера, за которым следует четкий описательный заголовок или заголовок. Соглашения относительно длины и содержания заголовка зависят от дисциплины. В точных науках допустимо длинное объяснение содержимого таблицы. В других дисциплинах заголовки должны быть описательными, но краткими, и любое объяснение или интерпретация данных должны иметь место в тексте. Обязательно найдите примеры из опубликованных статей по вашей дисциплине, которые вы можете использовать в качестве модели. Также полезно думать о заголовке как о «тематическом предложении» таблицы — он сообщает читателю, о чем эта таблица и как она организована. Таблицы читаются сверху вниз, поэтому заголовки располагаются над телом таблицы и выравниваются по левому краю.
Заголовки столбцов: цель заголовков столбцов состоит в том, чтобы упростить и прояснить таблицу, позволяя читателю быстро понять компоненты таблицы. Поэтому заголовки столбцов должны быть краткими и описательными и включать единицы анализа.
Поэтому заголовки столбцов должны быть краткими и описательными и включать единицы анализа.
Тело таблицы: здесь находятся ваши данные, независимо от того, являются ли они числовыми или текстовыми. Опять же, организуйте свою таблицу таким образом, чтобы помочь читателю понять значение данных. Обязательно подумайте о том, что вы хотите, чтобы ваши читатели сравнивали, и поместите эту информацию в столбец (вверх и вниз), а не в строку (поперек). Другими словами, составьте таблицу так, чтобы одинаковые элементы читались вниз, а не поперек. При использовании числовых данных с десятичными дробями убедитесь, что десятичные точки совпадают. Целые числа должны выстраиваться справа.
Прочие элементы стола
Таблицы должны быть помечены номером перед заголовком таблицы; таблицы и рисунки маркируются независимо друг от друга. Таблицы также должны иметь линии, разграничивающие различные части таблицы (заголовок, заголовки столбцов, данные и сноски, если они есть). Линии сетки или прямоугольники не должны быть включены в печатные версии.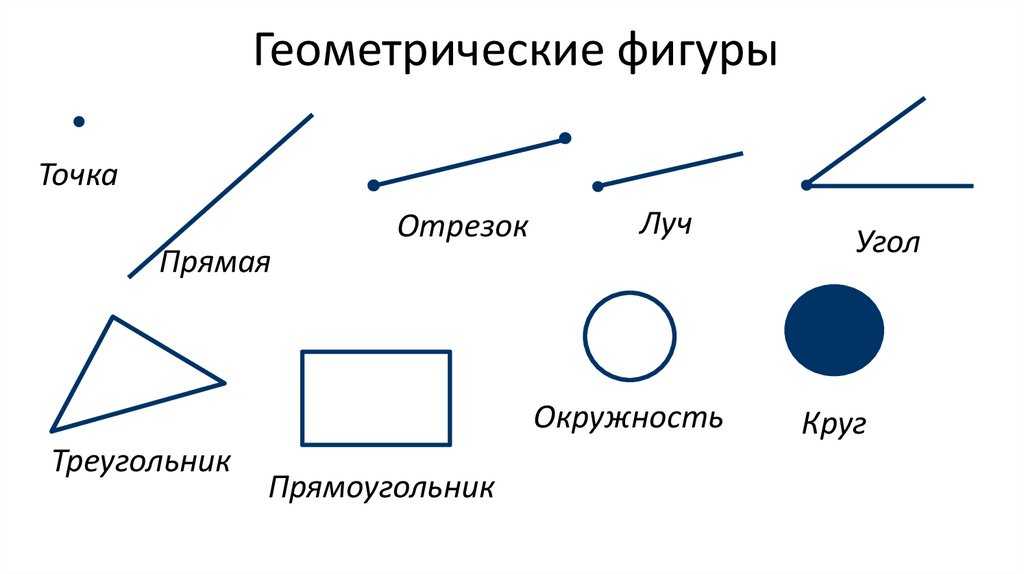 Таблицы могут включать или не включать другие элементы, такие как подзаголовки или сноски.
Таблицы могут включать или не включать другие элементы, такие как подзаголовки или сноски.
Краткий справочник по таблицам
Таблицы должны быть:
- По центру страницы.
- Нумеруются в порядке их появления в тексте.
- Ссылки в порядке их появления в тексте.
- Помечен номером таблицы и описательным заголовком над таблицей.
- Помечен метками столбцов и/или строк, которые описывают данные, включая единицы измерения.
- Отделить от самого текста; текст не обтекает таблицу.
Таблица 1. Физические характеристики Доктора в новой серии Доктор Кто
Высота | Возраст (лет) | |
Девятый Доктор | 6 футов 0 дюймов | 41 |
Десятый Доктор | 6 футов 1 дюйм | 35 |
Одиннадцатый Доктор | 5 футов 11 дюймов | 25 |
Таблица 2. Физические характеристики Доктора в новой серии Доктора Кто
Физические характеристики Доктора в новой серии Доктора Кто
Внешность | Гардероб | |
Девятый Доктор | Коротко подстриженные волосы Голубые глаза Чуть более коренастое телосложение | Черная кожаная куртка Темные рубашки с v-образным вырезом Черные армейские ботинки |
Десятый Доктор | Длинные спутанные волосы Карие глаза Очень тонкая конструкция | Тренч бежевый Костюм в тонкую полоску и галстук Чак Тейлорс |
Одиннадцатый Доктор | Более длинные волосы, зачесанные набок Зеленые глаза Чуть более коренастое телосложение | Коричневый твидовый жакет Галстук-бабочка и подтяжки Черные сапоги |
Использование цифр
Фигурки могут принимать разные формы.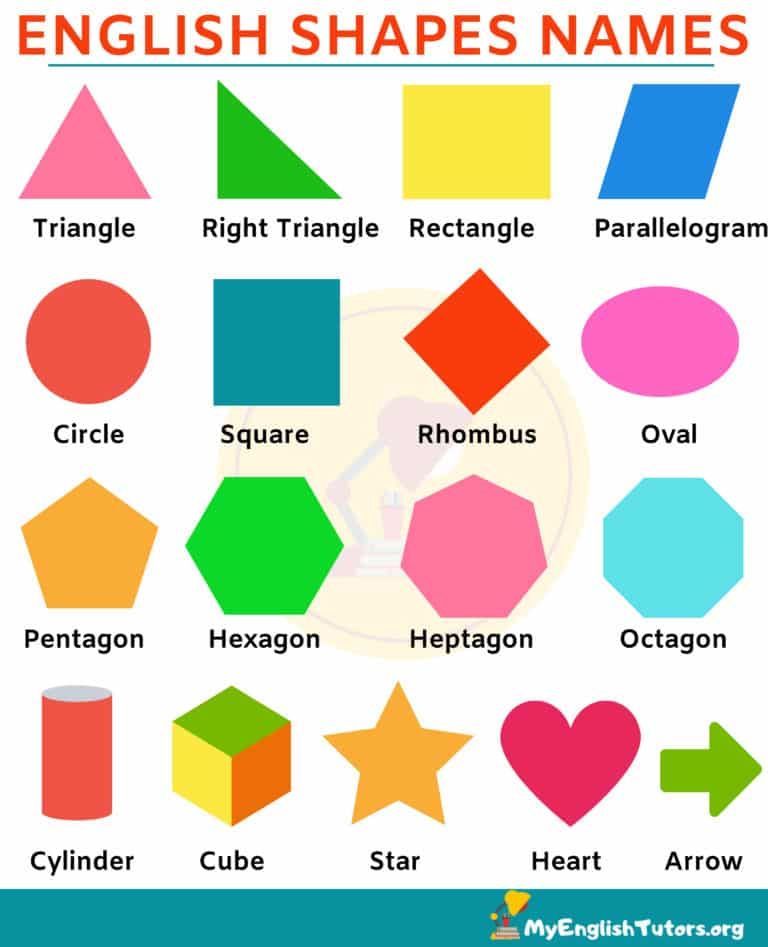 Это могут быть графики, диаграммы, фотографии, рисунки или карты. Тщательно подумайте о своей цели и руководствуйтесь здравым смыслом, чтобы выбрать наиболее эффективную фигуру для передачи основной мысли. Если вы хотите, чтобы ваш читатель понял пространственные отношения, карта или фотография могут быть лучшим выбором. Если вы хотите проиллюстрировать пропорции, поэкспериментируйте с круговой диаграммой или гистограммой. Если вы хотите проиллюстрировать взаимосвязь между двумя переменными, попробуйте линейный график или диаграмму рассеяния (подробнее о различных типах графиков ниже). Хотя существует много типов рисунков, таких как таблицы, у них есть некоторые общие черты: подписи, само изображение и любая необходимая контекстная информация (которая будет варьироваться в зависимости от типа используемого рисунка).
Это могут быть графики, диаграммы, фотографии, рисунки или карты. Тщательно подумайте о своей цели и руководствуйтесь здравым смыслом, чтобы выбрать наиболее эффективную фигуру для передачи основной мысли. Если вы хотите, чтобы ваш читатель понял пространственные отношения, карта или фотография могут быть лучшим выбором. Если вы хотите проиллюстрировать пропорции, поэкспериментируйте с круговой диаграммой или гистограммой. Если вы хотите проиллюстрировать взаимосвязь между двумя переменными, попробуйте линейный график или диаграмму рассеяния (подробнее о различных типах графиков ниже). Хотя существует много типов рисунков, таких как таблицы, у них есть некоторые общие черты: подписи, само изображение и любая необходимая контекстная информация (которая будет варьироваться в зависимости от типа используемого рисунка).
Подписи к рисункам
Рисунки должны быть помечены номером, за которым следует описательная подпись или название. Заголовки должны быть краткими, но исчерпывающими. Они должны описывать показанные данные, привлекать внимание к важным особенностям, содержащимся на рисунке, и иногда могут также включать интерпретацию данных. Рисунки обычно читаются снизу вверх, поэтому подписи располагаются под рисунком и выравниваются по левому краю.
Они должны описывать показанные данные, привлекать внимание к важным особенностям, содержащимся на рисунке, и иногда могут также включать интерпретацию данных. Рисунки обычно читаются снизу вверх, поэтому подписи располагаются под рисунком и выравниваются по левому краю.
Изображение
Наиболее важным фактором для фигур является простота. Выбирайте изображения, которые зритель может понять и интерпретировать четко и быстро. Учитывайте размер, разрешение, цвет и заметность важных функций. Рисунки должны быть достаточно большими и иметь достаточное разрешение, чтобы зритель мог разглядеть детали, не напрягая глаз. Также подумайте о том, какой формат в конечном итоге примет ваша статья. Журналы обычно публикуют цифры в черно-белом цвете, поэтому любая информация, закодированная цветом, будет потеряна для читателя. С другой стороны, цвет может быть хорошим выбором для документов, опубликованных в Интернете, или для презентаций PowerPoint. В любом случае используйте элементы фигуры, такие как цвет, линия и узор, для эффекта, а не для вспышки.
Дополнительная информация
Рисунки должны быть помечены номером перед заголовком таблицы; таблицы и рисунки нумеруются независимо друг от друга. Также не забудьте включить любую дополнительную контекстную информацию, необходимую вашему зрителю, чтобы понять рисунок. Для графиков это могут быть метки, легенда, поясняющая символы, а также вертикальные или горизонтальные деления. Для карт вам нужно указать масштаб и стрелку севера. Если вы не уверены в контекстуальной информации, ознакомьтесь с несколькими типами рисунков, которые обычно используются в вашей дисциплине.
Краткий справочник рисунков
Цифры должны быть:
- По центру страницы.
- Помечен (под рисунком) номером рисунка и соответствующим описательным заголовком («Рисунок» может быть написан по буквам [«Рисунок 1»] или сокращенно [«Рис. 1.»] при условии, что вы согласны).
- Нумеруются в порядке их появления в тексте.
- Ссылки в том порядке, в котором они появляются в тексте (т.
 е. на рисунок 1 ссылаются в тексте перед рисунком 2 и т. д.).
е. на рисунок 1 ссылаются в тексте перед рисунком 2 и т. д.). - Отделить от текста; текст не должен обтекать рисунки.
Графики
Каждый график — это рисунок, но не каждый рисунок — это график. Графики представляют собой определенный набор цифр, отображающих количественные отношения между переменными. Некоторые из наиболее распространенных графиков включают гистограммы, частотные гистограммы, круговые диаграммы, точечные диаграммы и линейные графики, каждый из которых по-разному отображает тенденции или взаимосвязи внутри наборов данных и между ними. Вам нужно будет тщательно выбрать лучший график для ваших данных и отношений, которые вы хотите показать. Более подробная информация о некоторых распространенных типах графиков приведена ниже. Хороший совет по построению графиков — делать их простыми. Помните, что основной целью вашего графика является общение. Если ваш зритель не может визуально декодировать ваш график, значит, вы не смогли передать содержащуюся в нем информацию.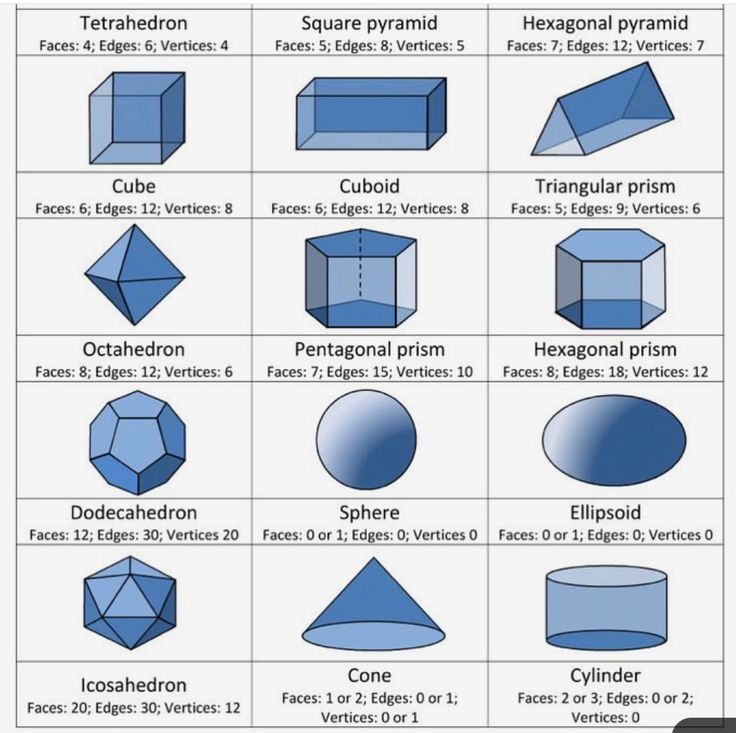
Круговые диаграммы
Круговые диаграммы используются для отображения относительных пропорций, в частности отношения нескольких частей к целому. Используйте круговые диаграммы только в том случае, если части круговой диаграммы являются взаимоисключающими категориями, а сумма частей составляет значимое целое (100% чего-либо). Круговые диаграммы хорошо показывают отношения «в целом» (т. е. некоторые категории составляют «много» или «мало» всего). Однако, если вы хотите, чтобы ваш читатель различал мелкие различия в ваших данных, круговая диаграмма не для вас. Люди не очень хороши в сравнении, основанном на ракурсах. Мы намного лучше сравниваем длину, поэтому попробуйте гистограмму как альтернативный способ показать относительные пропорции. Кроме того, круговые диаграммы с большим количеством маленьких сегментов или сегментов очень разных размеров трудно читать, поэтому ограничьте свои категории до 5-7 категорий.
Примеры плохих круговых диаграмм:
Рисунок 1. Элементы в марсианском грунте
Элементы в марсианском грунте
На диаграмме показано относительное соотношение пятнадцати элементов в марсианском грунте, перечисленных в порядке от «наибольшего» к «наименьшему»: кислород, кремний, железо, магний, кальций, сера, алюминий, натрий, калий, хлор, гелий, азот, фосфор, бериллий и др. Кислород составляет около ⅓ состава, а кремний и железо вместе составляют около ¼. Остальные срезы составляют меньшие пропорции, но проценты не указаны в ключе и их трудно оценить. Также трудно различить пятнадцать цветов при сравнении круговой диаграммы с ключом с цветовой кодировкой.
Рисунок 2. Досуг венерианских подростков
На диаграмме показано относительное соотношение пяти видов досуга венерианских подростков (загар, поездки на Марс, чтение, возня со спутниками и воровство земного кабеля). Хотя каждый из пяти кусочков примерно одинакового размера (примерно 20 % от общего числа), процент венерианских подростков, занимающихся каждым видом деятельности, сильно различается (загар: 80 %, полеты на Марс: 40 %, чтение: 12 %, месиво).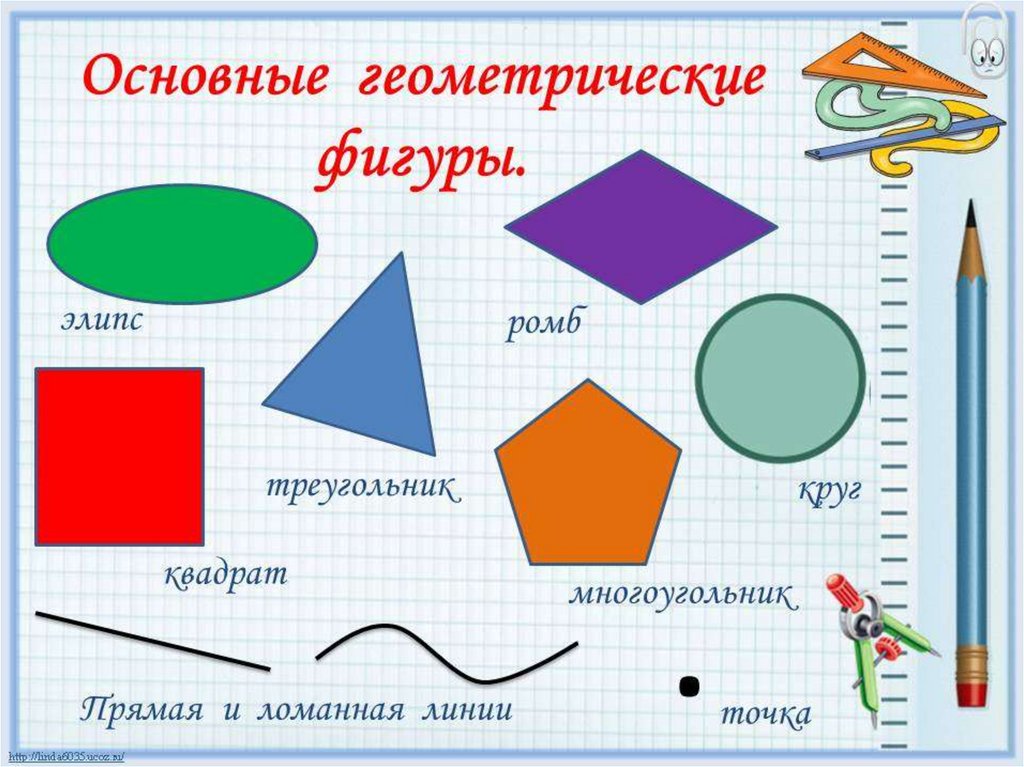 со спутниками: 30%, кража кабеля Земли: 77%). Следовательно, существует несоответствие между метками и фактической долей, представленной каждым действием (другими словами, если чтение составляет 12% от общего числа, его срез должен занимать 12% площади круговой диаграммы), что делает представление неточным. . Кроме того, метки для пяти срезов в сумме дают 239% (а не 100%), что делает невозможным точное представление этого набора данных с помощью круговой диаграммы.
со спутниками: 30%, кража кабеля Земли: 77%). Следовательно, существует несоответствие между метками и фактической долей, представленной каждым действием (другими словами, если чтение составляет 12% от общего числа, его срез должен занимать 12% площади круговой диаграммы), что делает представление неточным. . Кроме того, метки для пяти срезов в сумме дают 239% (а не 100%), что делает невозможным точное представление этого набора данных с помощью круговой диаграммы.
Гистограммы
Гистограммы также используются для отображения пропорций. В частности, они полезны для демонстрации связи между независимыми и зависимыми переменными, когда независимые переменные представляют собой дискретные (часто номинальные) категории. Некоторыми примерами являются род занятий, пол и вид. Гистограммы могут быть вертикальными или горизонтальными. На вертикальной гистограмме независимая переменная отображается по оси х (слева направо), а зависимая переменная — по оси у (вверх и вниз). В горизонтальной зависимая переменная будет показана на горизонтальной оси (x), независимая на вертикальной оси (y).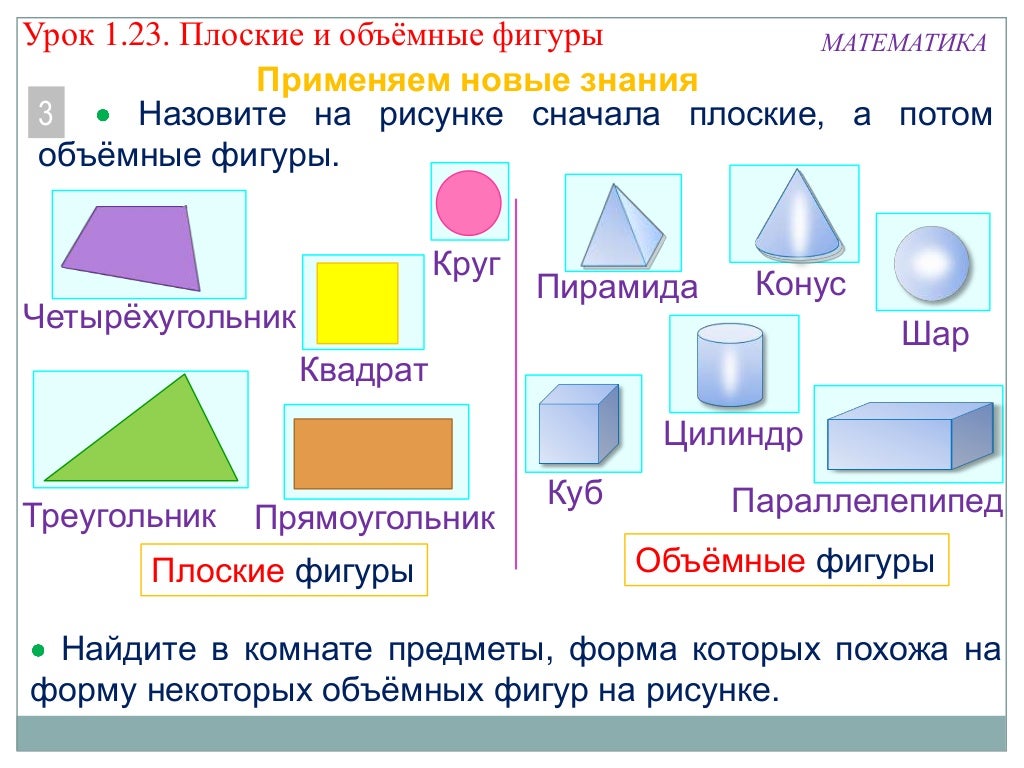 Масштаб и начало графика должны быть осмысленными. Если зависимая (числовая) переменная имеет естественную нулевую точку, она обычно используется в качестве исходной точки для гистограммы. Однако ноль — не всегда лучший выбор. Вам следует поэкспериментировать как с источником, так и с масштабом, чтобы наилучшим образом показать соответствующие тенденции в ваших данных, не вводя зрителя в заблуждение с точки зрения силы или степени этих тенденций.
Масштаб и начало графика должны быть осмысленными. Если зависимая (числовая) переменная имеет естественную нулевую точку, она обычно используется в качестве исходной точки для гистограммы. Однако ноль — не всегда лучший выбор. Вам следует поэкспериментировать как с источником, так и с масштабом, чтобы наилучшим образом показать соответствующие тенденции в ваших данных, не вводя зрителя в заблуждение с точки зрения силы или степени этих тенденций.
Пример гистограммы:
Рисунок 3. Пол членов экипажа космического корабля в популярном телесериале
На графике показано количество мужчин и женщин в составе экипажа космического корабля для пяти различных популярных телесериалов: «Звездный путь» (1965 г.), «Звездный крейсер» (1978 г.), «Звездный путь: TNG» (1987 г.), «Звездные врата SG-1» (1997 г.) и «Светлячок» ( 2002). Поскольку телесериалы расположены по оси x в хронологическом порядке, график также можно использовать для поиска тенденций этих чисел во времени.
Несмотря на то, что количество членов съемочной группы для каждого шоу одинаково (от 9 до 11), соотношение женщин и мужчин в съемочной группе различается. В «Звездном пути» женщин в команде вдвое меньше, чем мужчин (3 и 6 соответственно), в «Звездном крейсере» женщин в четыре раза меньше, чем мужчин (2 и 9 соответственно), в «Звездном пути: TNG» четыре члена экипажа женского пола и шесть членов экипажа мужского пола, в Stargate SG-1 в два раза меньше членов экипажа женского пола, чем в экипаже мужского пола (3 и 7 соответственно), а в Firefly четыре члена женского и пять мужского экипажа.
Частотные гистограммы/распределения
Частотные гистограммы представляют собой гистограммы особого типа, которые показывают взаимосвязь между независимыми и зависимыми переменными, где независимая переменная является непрерывной, а не дискретной. Это означает, что каждая полоса представляет диапазон значений, а не одно наблюдение. Зависимые переменные в гистограмме всегда являются числовыми, но могут быть абсолютными (числа) или относительными (проценты). Частотные гистограммы хороши для описания популяций — примеры включают распределение баллов по экзаменам для учащихся в классе или возрастное распределение людей, живущих в Чапел-Хилл. Вы можете поэкспериментировать с диапазонами столбцов (также известными как «ячейки») для достижения наилучшего уровня детализации, но каждый диапазон или ячейка должны иметь одинаковую ширину и четко обозначены.
Частотные гистограммы хороши для описания популяций — примеры включают распределение баллов по экзаменам для учащихся в классе или возрастное распределение людей, живущих в Чапел-Хилл. Вы можете поэкспериментировать с диапазонами столбцов (также известными как «ячейки») для достижения наилучшего уровня детализации, но каждый диапазон или ячейка должны иметь одинаковую ширину и четко обозначены.
Диаграммы рассеяния XY
Диаграммы рассеяния — еще один способ проиллюстрировать взаимосвязь между двумя переменными. В этом случае данные отображаются в виде точек в системе координат x,y, где каждая точка представляет одно наблюдение по двум осям вариации. Часто точечные диаграммы используются для иллюстрации корреляции между двумя переменными: по мере увеличения одной переменной увеличивается и другая (положительная корреляция) или уменьшается (отрицательная корреляция). Однако корреляция не обязательно означает, что изменения одной переменной вызывают изменения другой. Например, третья переменная, не нанесенная на график, может быть причиной обоих.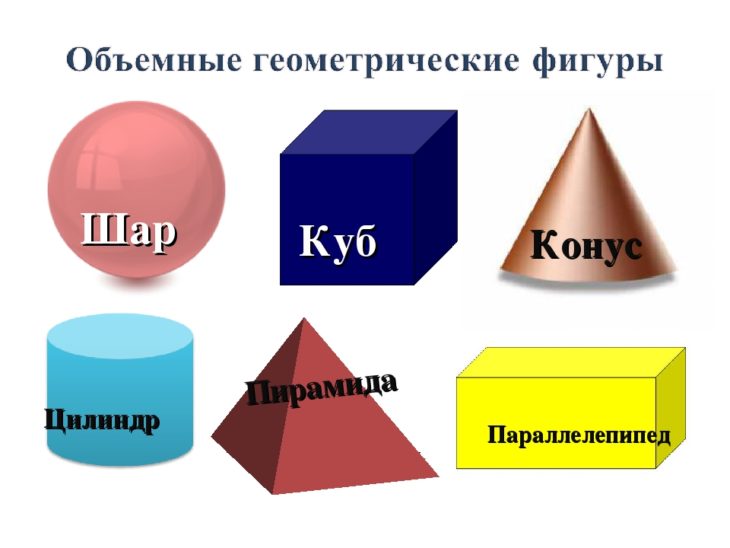 Другими словами, точечные диаграммы можно использовать для построения графика одной независимой и одной зависимой переменной или для построения графика двух независимых переменных. В случаях, когда одна переменная зависит от другой (например, рост частично зависит от возраста), нанесите независимую переменную на горизонтальную ось (x), а зависимую переменную на вертикальную ось (y). В дополнение к корреляции (линейной зависимости) диаграммы рассеяния можно использовать для построения нелинейных связей между переменными.
Другими словами, точечные диаграммы можно использовать для построения графика одной независимой и одной зависимой переменной или для построения графика двух независимых переменных. В случаях, когда одна переменная зависит от другой (например, рост частично зависит от возраста), нанесите независимую переменную на горизонтальную ось (x), а зависимую переменную на вертикальную ось (y). В дополнение к корреляции (линейной зависимости) диаграммы рассеяния можно использовать для построения нелинейных связей между переменными.
Пример точечной диаграммы:
Рисунок 4. Влияние погоды на появление НЛО
Точечная диаграмма показывает зависимость между температурой (ось X, независимая переменная) и количеством наблюдений НЛО (ось Y, зависимая переменная) для 53 отдельных точек данных. Температура колеблется от 0°F до 120°F, а количество наблюдений НЛО колеблется от 1 до 10. На графике показано небольшое количество наблюдений НЛО (от 1 до 4) при температуре ниже 80°F и большое количество наблюдений НЛО. более широкий диапазон количества наблюдений (от 1 до 10) при температуре выше 80°F. Похоже, что количество наблюдений имеет тенденцию к увеличению с повышением температуры, хотя во многих случаях при высоких температурах происходит лишь несколько наблюдений.
более широкий диапазон количества наблюдений (от 1 до 10) при температуре выше 80°F. Похоже, что количество наблюдений имеет тенденцию к увеличению с повышением температуры, хотя во многих случаях при высоких температурах происходит лишь несколько наблюдений.
Линейные графики XY
Линейные графики аналогичны точечным диаграммам тем, что они отображают данные по двум осям вариации. Линейные графики, однако, отображают ряд связанных значений, отображающих изменение одной переменной в зависимости от другой, например, населения мира (зависимое) с течением времени (независимое). Отдельные точки данных соединяются линией, привлекая внимание зрителя к локальным изменениям между соседними точками, а также к более крупным тенденциям в данных. Линейные графики похожи на гистограммы, но лучше показывают скорость изменения между двумя точками. Линейные графики также можно использовать для сравнения нескольких зависимых переменных путем нанесения нескольких линий на один и тот же график.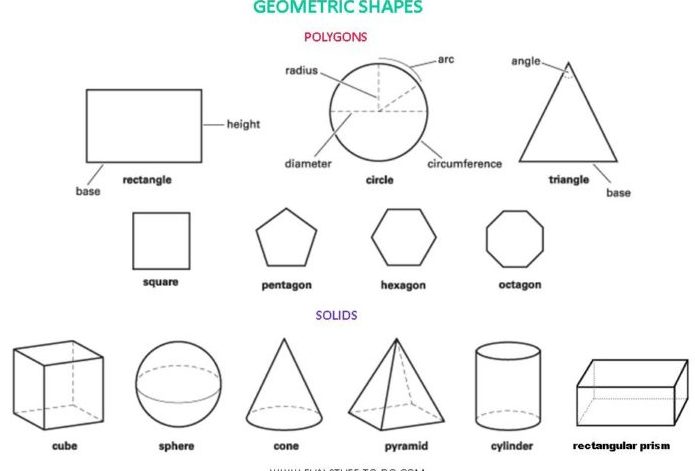
Пример линейного графика XY:
Рисунок 5. Возраст актера каждой регенерации Доктора Кто (1-11)
Линейный график показывает возраст (в годах) актера каждой регенерации Доктора Кто с первой по одиннадцатую регенерацию. Возраст варьируется от максимума около 55 лет в первой регенерации до минимума около 25 лет в одиннадцатой регенерации. Существует тенденция к снижению возраста актеров в течение одиннадцати регенераций.
Общие советы по графикам
Стремитесь к простоте. Ваши данные будут сложными. Не поддавайтесь искушению передать сложность ваших данных в графической форме. Ваша работа (и работа вашего графика) состоит в том, чтобы сообщать самое важное о данных. Думайте о графиках так же, как вы думаете о абзацах: если вам нужно сказать несколько важных вещей о ваших данных, сделайте несколько графиков, каждый из которых подчеркивает один важный момент, который вы хотите подчеркнуть.
Стремитесь к ясности. Убедитесь, что ваши данные представлены визуально четким образом. Убедитесь, что вы ясно объяснили элементы графика. Учитывайте свою аудиторию. Будет ли ваш читатель знаком с типом фигуры, которую вы используете (например, с коробчатой диаграммой)? Если нет, или если вы не уверены, вам может потребоваться объяснить правила построения коробчатых диаграмм в тексте. Избегайте «харт-мусора». Лишние элементы только делают графики визуально запутанными. Ваш читатель не захочет тратить 15 минут на выяснение точки вашего графика.
Убедитесь, что вы ясно объяснили элементы графика. Учитывайте свою аудиторию. Будет ли ваш читатель знаком с типом фигуры, которую вы используете (например, с коробчатой диаграммой)? Если нет, или если вы не уверены, вам может потребоваться объяснить правила построения коробчатых диаграмм в тексте. Избегайте «харт-мусора». Лишние элементы только делают графики визуально запутанными. Ваш читатель не захочет тратить 15 минут на выяснение точки вашего графика.
Стремитесь к точности. Внимательно проверьте свой график на наличие ошибок. Даже простая графическая ошибка может изменить смысл и интерпретацию данных. Используйте графики ответственно. Не манипулируйте данными так, чтобы казалось, что они говорят что-то, чего на самом деле нет — сообразительные зрители разгадают эту уловку, и в лучшем случае вы будете выглядеть некомпетентным, а в худшем — нечестным.
Как таблицы и рисунки должны взаимодействовать с текстом?
Расположение рисунков и таблиц в тексте зависит от дисциплины.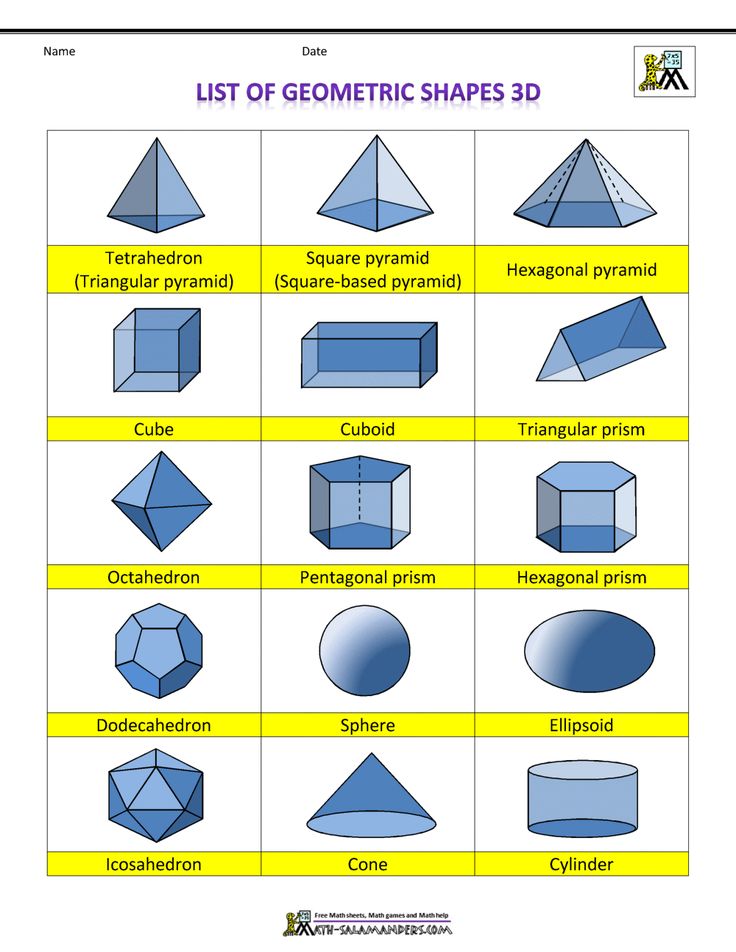 В рукописях (таких как лабораторные отчеты и черновики) принято размещать таблицы и рисунки на отдельных страницах от текста, как можно ближе к тому месту, где вы впервые на них ссылаетесь. Вы также можете поместить все рисунки и таблицы в конец статьи, чтобы не разбивать текст. Рисунки и таблицы также могут быть встроены в текст, если сам текст не разбит на небольшие фрагменты. Комплексные необработанные данные обычно представлены в приложении. Обязательно проверьте правила размещения рисунков и таблиц в вашей дисциплине.
В рукописях (таких как лабораторные отчеты и черновики) принято размещать таблицы и рисунки на отдельных страницах от текста, как можно ближе к тому месту, где вы впервые на них ссылаетесь. Вы также можете поместить все рисунки и таблицы в конец статьи, чтобы не разбивать текст. Рисунки и таблицы также могут быть встроены в текст, если сам текст не разбит на небольшие фрагменты. Комплексные необработанные данные обычно представлены в приложении. Обязательно проверьте правила размещения рисунков и таблиц в вашей дисциплине.
Вы можете использовать текст, чтобы помочь читателю интерпретировать информацию, содержащуюся в рисунке, таблице или графике, — сообщите читателю, что передает рисунок или таблица и почему было важно их включить.
При обращении к таблицам и графикам в тексте вы можете использовать:
- Пункты, начинающиеся с «как»: «Как показано в таблице 1, …»
- Пассивный залог: «Результаты представлены в таблице 1».
- Активный голос (если подходит для вашей дисциплины): «Таблица 1 показывает, что…»
- Скобки: «Каждый образец дал положительный результат на три питательных вещества (таблица 1)».

Консультационные работы
Мы обращались к этим работам, когда писали этот раздаточный материал. Это не исчерпывающий список ресурсов по теме раздаточного материала, и мы рекомендуем вам провести собственное исследование, чтобы найти дополнительные публикации. Пожалуйста, не используйте этот список в качестве модели для формата вашего собственного списка литературы, так как он может не соответствовать используемому вами стилю цитирования. Руководство по форматированию ссылок см. в руководстве по цитированию библиотек UNC. Мы периодически пересматриваем эти советы и приветствуем обратную связь.
Американская психологическая ассоциация. 2010. Руководство по публикации Американской психологической ассоциации . 6-е изд. Вашингтон, округ Колумбия: Американская психологическая ассоциация.
Колледж Бейтса. 2012. « Почти все, что вы хотели знать о создании таблиц и рисунков». Как написать статью в стиле и формате научного журнала , 11 января 2012 г. http://abacus.bates.edu/~ganderso/biology/resources/writing/HTWtablefigs.html.
http://abacus.bates.edu/~ganderso/biology/resources/writing/HTWtablefigs.html.
Кливленд, Уильям С. 1994. Элементы графических данных , 2-е изд. Саммит, Нью-Джерси: Hobart Press..
Совет научных редакторов. 2014. Научный стиль и формат: Руководство CSE для авторов, редакторов и издателей , 8-е изд. Чикаго и Лондон: Издательство Чикагского университета.
Издательство Чикагского университета. 2017. Чикагское руководство по стилю , 17-е изд. Чикаго и Лондон: Издательство Чикагского университета.
Эта работа находится под лицензией Creative Commons Attribution-NonCommercial-NoDerivs 4.0 License.
Вы можете воспроизводить его для некоммерческого использования, если вы используете весь раздаточный материал и указываете источник: The Writing Center, University of North Carolina at Chapel Hill
Сделать подарок
графика — Рисунок в виде ?? на обороте — TeX
спросил
Изменено
1 год, 11 месяцев назад
Просмотрено
315 раз
Я следил за учебными пособиями в Интернете, такими как https://latex-tutorial. com/tutorials/figures/ и https://www.overleaf.com/learn/latex/How_to_Write_a_Thesis_in_LaTeX_(Part_3):_Рисунки,_Подрисунки_и_Таблицы#Таблицы
com/tutorials/figures/ и https://www.overleaf.com/learn/latex/How_to_Write_a_Thesis_in_LaTeX_(Part_3):_Рисунки,_Подрисунки_и_Таблицы#Таблицы
для создания фигур, на которые можно ссылаться, в моем документе, но все, что выводится, это ?? вместо фигуры.
Вот импортированные пакеты:
\usepackage[utf8]{inputenc}
\usepackage{booktabs} % для улучшения внешнего вида таблиц
\usepackage{array} % для лучших массивов (например, матриц) в математике
\usepackage{paralist} % очень гибкие и настраиваемые списки (например, перечисление/детализация и т. д.)
\usepackage{verbatim} % добавляет среду для комментирования блоков текста и для лучшего дословного воспроизведения
\usepackage{subfig} % позволяют включать более одного рисунка/таблицы с подписью в один поплавок
\usepackage{мультикол}
\usepackage[a4paper, total={8in, 8in}]{геометрия}
\usepackage{приложение}
\usepackage{таблицаx}
\usepackage{biblatex}%для цитирования статей
\usepackage{fancyhdr}
\addbibresource{ACS231.bib}%изменить имя файла на другой файл . bib
\usepackage{graphicx}
\usepackage{комментарий}
\graphicspath{ {./images/} }
bib
\usepackage{graphicx}
\usepackage{комментарий}
\graphicspath{ {./images/} }
Дальше по документу:
\begin{document}
\begin{мультиколы}{2}
\subsection{Дизайн электроники | Упражнение 9}
Вот электрическая схема.
\begin{рисунок}[ч!]
\центрирование
\includegraphics[ширина=7см]{finalSchematic.jpg}
\caption{Схема}
\label{рис:схема}
\конец{рисунок}
\figurename{\ref{рис:схема}}
\ref{рис.:схема}
\конец{документ}
\end{многостолбцы}{2}
Я попробовал это в примере программы в Overleaf, и это сработало, предполагая, что дело не в самом файле.
Я склонен думать, что это может быть взаимодействие пакетов. Я создал новый файл и вставил весь код, который вызвал ту же проблему. Я видел, как проблема возникает из-за неправильного синтаксиса в других сообщениях, но если это сработало в файле примера, это не означает, что это проблема синтаксиса. Есть идеи?
Журнал показывает это:
Не появляются красные круги, только желтое предупреждение, соответствующее журналу. Строка, на которую он ссылается:
Строка, на которую он ссылается:
\ref{fig:schematic}
, который, как мне кажется, относится к чему-то, что на самом деле помечено?
- графика
- оглавление
- многоколоночный
- импорт
1
Ни один из пакетов, которые вы показываете, не связан с \ref (см. ниже о multicol ). \figurename превращает текст в цифру (или ее перевод) почти во всех классах, где есть цифры, поэтому очень удивительно, что вы получаете ?? без префикса цифра или что вы получаете только один ?? не два, если у вас есть два экземпляра \ref . Необычно, но не является ошибкой явное использование \figurename .
Вы уверены, что ошибок не было показано?0005
Дано
\documentclass{статья}
\usepackage{graphicx}
\начать{документ}
\subsection{Дизайн электроники | Упражнение 9}
Вот электрическая схема. \begin{рисунок}[ч!]
\центрирование
\includegraphics[width=7cm]{example-image.jpg}
\caption{Схема}
\label{рис:схема}
\конец{рисунок}
\figurename{\ref{рис:схема}}
\ref{рис.:схема}
\конец{документ}
\begin{рисунок}[ч!]
\центрирование
\includegraphics[width=7cm]{example-image.jpg}
\caption{Схема}
\label{рис:схема}
\конец{рисунок}
\figurename{\ref{рис:схема}}
\ref{рис.:схема}
\конец{документ}
после первого запуска должно выглядеть как
после второго запуска должно выглядеть как
Ваш обновленный вопрос показывает причину:
Если я добавлю multicol в пример, я получу то же предупреждение и тот же результат:
\documentclass{article}
\usepackage{graphicx,multicol}
\начать{документ}
\begin{мультиколы}{2}
\subsection{Дизайн электроники | Упражнение 9}
Вот электрическая схема.
\begin{рисунок}[ч!]
\центрирование
\includegraphics[width=7cm]{example-image.jpg}
\caption{Схема}
\label{рис:схема}
\конец{рисунок}
\figurename{\ref{рис:схема}}
\ref{рис.:схема}
\end{многостолбцы}
\конец{документ}
Поскольку вы использовали цифру, где цифры не разрешены, она по существу отбрасывается, поэтому \метка никогда не была активирована, и поэтому \ref сообщает об этом как о неопределенной метке.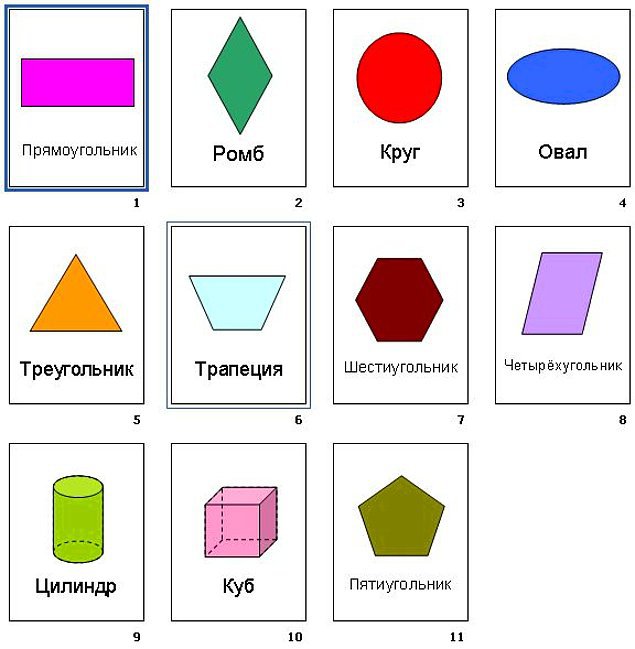
3
Мультиколлы и цифры, упомянутые в другом ответе, борются за совместимость:
Поскольку вы использовали фигуру, где цифры не разрешены, она по существу отбрасывается, поэтому \label никогда не была активирована, и поэтому \ref сообщает о ней как о неопределенной метке.
Следуя предложенному здесь ответу: многоцветность и цифры
Мне удалось использовать код, предложенный как для ссылки, так и для отображения рисунка.
Я добавил это в начало документа под \usepackage :
\newenvironment{Рисунок}
{\par\medskip\noindent\minipage{\linewidth}}
{\ endminipage \ пар \ медскип}
и это для отображения и ссылки на рисунок:
\begin{Рисунок}
\центрирование
\includegraphics[width=\linewidth]{Изображения/finalSchematic.jpg}
\captionof{figure}{Электронные схемы}
\label{фигсхема}
\end{Рисунок}%Capital F. Используйте заголовок.



 е. на рисунок 1 ссылаются в тексте перед рисунком 2 и т. д.).
е. на рисунок 1 ссылаются в тексте перед рисунком 2 и т. д.).
 bib
\usepackage{graphicx}
\usepackage{комментарий}
\graphicspath{ {./images/} }
bib
\usepackage{graphicx}
\usepackage{комментарий}
\graphicspath{ {./images/} }
 \begin{рисунок}[ч!]
\центрирование
\includegraphics[width=7cm]{example-image.jpg}
\caption{Схема}
\label{рис:схема}
\конец{рисунок}
\figurename{\ref{рис:схема}}
\ref{рис.:схема}
\конец{документ}
\begin{рисунок}[ч!]
\центрирование
\includegraphics[width=7cm]{example-image.jpg}
\caption{Схема}
\label{рис:схема}
\конец{рисунок}
\figurename{\ref{рис:схема}}
\ref{рис.:схема}
\конец{документ}